【文档说明】2021年高中数学人教版必修第一册：4.5《函数的应用（二）》精品讲义(含解析).doc，共(12)页，692.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31245.html

以下为本文档部分文字说明：

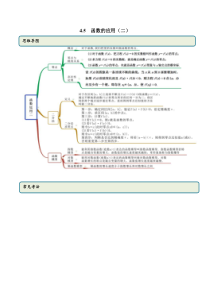
4.5函数的应用（二）思维导图常见考法考点一零点的求解【例1】（2020·武威第六中学高二期末（文））若函数()fxaxb的零点是2（0a），则函数2()gxaxbx的零点是（）A．2B．2和0C．0D．2和0【答案】B【解析

】由条件知(2)0f，∴2ba，∴2()(2)gxaxbxaxx的零点为0和2.故选B.【一隅三反】1．（2020·全国高三课时练习（理））已知函数f(x)＝22111log1xxxx

，，，则函数f(x)的零点为（）A．，0B．－2，0C．D．0【答案】D【解析】当1x时，令f(x)＝2x－1＝0，解得x＝0；当1x时，令f(x)＝1＋log2x＝0，解得x＝12，又因为1x

，所以此时方程无解.综上所述，函数f(x)的零点只有0.故选：D（1）代数法：根据零点的定义，解方程()0fx，它的实数解就是函数()yfx的零点.（2）几何法：若方程()0fx无法求解，可以根据函数()yfx的性质及图象求出零点.2.已知函数221,1()1log,1xxf

xxx，则函数()fx的零点为________．【答案】0【解析】当1x时，由()210xfx，解得0x；当1x时，由2()1log0fxx，解得12x，又因为1x，所以此时方程无解．综上，函数()fx的零点为0.考点二零点区间的判断【例2】（202

0·湖南娄底·高二期末）函数3()ln9fxxx的零点所在的区间为（）A．(0,1)B．(1,2)C．(2,3)D．(3,4)【答案】C【解析】可以求得，所以函数的零点在区间(2,3)内．故选C．【一隅三反】1．（2020·宁县第二中学高二期中（文））函数f(x)=23xx的零点所

在的一个区间是A．（-2，-1）B．（-1,0）C．（0,1）D．（1,2）【答案】B【解析】因为函数f(x)=2x+3x在其定义域内是递增的，那么根据f(-1)=153022,f（0）=1+0=1>0,那么函数的零点存在性定理可知，函数的零点的区间为（-1,0），选B．2．

（2020·甘肃省岷县第一中学高二月考（文））函数1()22xfxx的零点所在区间为（）判断函数零点所在区间的三个步骤(1)代入：将区间端点值代入函数求出函数的值．(2)判断：把所得的函数值相乘，并进行符号判

断．(3)结论：若符号为正且函数在该区间内是单调函数，则在该区间内无零点，若符号为负且函数连续，则在该区间内至少有一个零点．A．(1,0)B．(0,1)C．(1,2)D．(2,3)【答案】D【解析】12125f，01023f，1311222f

，1122244f，1733288f，230ff，由零点存在定理可知：fx零点所在区间为2,3.故选：D.3．（2020·浙江衢州·高一期末）函数24xf

xx的零点所在的区间是（）A．1,0B．2,3C．0,1D．1,2【答案】D【解析】19114022f，010430f，121410f，242420f，38347f

120fffx零点所在区间为1,2故选：D考点三零点个数的判断【例3】（1）（2020·哈尔滨市第十二中学校高二期末（文））函数212log6yxx的零点个数为（）

A．0个B．1个C．2个D．3个（2）（2020·山东省枣庄市第十六中学高一期中）方程0lnxx的实数解的个数为（）A．1B．2C．3D．0【答案】（1）C（2）A【解析】（1）令0y，则212log60xx，即250x

x，又Δ1200，故该方程有两根，且均满足函数定义域.故该函数有两个零点.故选：C（2）方程0lnxx的实数解的个数，即为方程lnxx的实数解的个数，即为函数lnyx与函数yx图象的交点的个数，在同一坐标系中作出函数lnyx与

函数yx的图象，如图所示：只有一个交点，所以方程0lnxx的实数解的个数为1故选：A【一隅三反】1．（2020·四川内江·高三三模（理））函数2ln14xfxx的零点个数为_______.【答案】2【解析】令2ln140xfxx

，则24ln122xxx，在同一直角坐标系中作出函数ln1yx与22xy的图象，如图：由图象可知，函数ln1yx当1x时，ln1yx则与22xy的图象有必有两

个交点，所以方程24ln122xxx有两个不同实根，所以函数2ln14xfxx的零点个数为2.判断函数零点个数的三种方法(1)方程法：若方程f(x)＝0的解可求或能判断解的个数，可

通过方程的解来判断函数是否存在零点或判定零点的个数．(2)图象法：由f(x)＝g(x)－h(x)＝0，得g(x)＝h(x)，在同一坐标系内作出y1＝g(x)和y2＝h(x)的图象，根据两个图象交点的个数来判定函数零点

的个数．(3)定理法：函数y＝f(x)的图象在区间[a，b]上是一条连续不断的曲线，由f(a)·f(b)<0即可判断函数y＝f(x)在区间(a，b)内至少有一个零点．若函数y＝f(x)在区间(a，b)上是单调函数，则函数f(x)在区间(a，b)内只有一个零点．故答案为：2.2．（2020·浙江高一

课时练习）方程21lg22xx的实根的个数为________．【答案】2个【解析】方程21lg22xx的实根个数可转为函数2122yx和lgyx的交点个数，在同一坐标系中作出2122yx和lgyx

的图像，如图，可得交点个数为2个，故方程的实根个数是2个，故答案为：2个3.已知01a，则函数logxayax的零点的个数为______.【答案】2【解析】函数logxayax的零点的个数即为方程logxaax的解的个数，也就是函数()(01)xfxaa与(

)log(01)agxxa的图象的交点的个数.画出函数图象如图所示，观察可得函数()(01)xfxaa与()log(01)agxxa的图象的交点的个数为2，从而函数logxayax的零点的个数为2考点四根据零点求参数【例4】．（2020·山西应

县一中高二期中（文））已知关于x的方程21xm有两个不等实根，则实数m的取值范围是（）A．(,1]B．,1C．[1,)D．1,【答案】D【解析】由题意,画出2xfxm的图像如下图所示:由图像

可知,若方程21xm有两个不等实根则函数图像在y轴左侧的最大值大于等于1即可所以1m>即(1,)m故选:D【一隅三反】1．（2020·江苏省海头高级中学高一月考）方程222(1)3110xkxk有两个不相等的实数根，则实数k的

取值范围为（）A．(,3)(2,)B．(3,2)C．(2,3)D．(,2)(3,)【答案】B【解析】方程222(1)3110xkxk中，令0，得224(1)4(311)0kk，化简得260kk，解得32k，所以(3,2)k

时，方程有两个不相等的实数根；故选：B.2．（2020·内蒙古集宁一中高二月考（文））若函数()27xfxx的零点所在的区间为(,1)()kkkZ,则k=()A．3B．4C．1D．2【答案】D【解析】∵(2)4270,(3)83

70,ff且()fx单调递增,∴()fx的零点所在的区间为（2,3）,∴2k.故选：D3．函数f(x)＝x2－2|x|＋a－1有四个不同的零点，求实数a的取值范围．【答案】(1,2)【解析】由f(

x)＝0得a－1＝2|x|－x2，因为函数f(x)＝x2－2|x|＋a－1有四个不同的零点，所以函数y＝a－1与y＝2|x|－x2的图象有四个交点，画出函数y＝2|x|－x2的图象，如图所示，观察图象可知，0<

a－1<1，所以1<a<2.即a的取值范围为(1,2)．考点五二分法【例5】（2020·福建高一期中）设()338xfxx，用二分法求方程3380xx在(1,2)x内近似解的过程中得10f

，1.50f，1.250f，则方程的根落在区间()A．(1,1.25)B．(1.25,1.5)C．(1.5,2)D．不能确定【答案】B【解析】()338xfxx又(1.5)0,(1.25)0ff(1.5)(

1.25)0ff由零点存在定理可得()fx在区间(1.25,1.5)存在零点.3380xx方程的根落在区间(1.25,1.5)故选：B．【一隅三反】1．（2020·全国高一单元测试）在用“二分法”求函数f(x)零点近似值时，第

一次所取的区间是[－2,4]，则第三次所取的区间可能是()A．[1,4]B．[－2,1]二分法的适用条件判断一个函数能否用二分法求其零点的依据是：其图象在零点附近是连续不断的，且该零点为变号零点．因此，用二分法求函数的零点近似值的方法仅对函数的变号零点适用

，对函数的不变号零点不适用．C．5[2,]2D．1[,1]2【答案】D【解析】∵第一次所取的区间是[－2,4]，∴第二次所取的区间可能为[－2,1]，[1,4]，∴第三次所取的区间可能为1155[2,],[,1],[1,],[,4]2222.2．（202

0·浙江高一单元测试）利用计算器，列出自变量的函数值的对应值如下表：0.20.61.01.41.82.22.63.03.4…1.1491.5162.02.6393.4824.5956.0638.010.556…0.040.361.01.96

3.244.846.769.011.56…那么方程的一个根位于下列区间（）A．（0.6，1.0）B．（1.4，1.8）C．（1.8，2.2）D．（2.6，3.0）【答案】C【解析】构造f(x)＝2x－x2，则f(1.

8)＝0.242，f(2.2)＝－0.245，故在(1.8,2.2)内存在一点使f(x)＝2x－x2＝0，所以方程2x＝x2的一个根就位于区间(1.8,2.2)上．选C3．（2019·海南龙华·海口一中高二月考）下列函数图像与x轴均有公共

点，其中能用二分法求零点的是()A．B．C．D．【答案】C【解析】解：能用二分法求零点的函数必须在给定区间[a，b]上连续不断，并且有f（a）•f（b）＜0A、B中不存在f（x）＜0，D中函数不连续．故选C．考法六函数模型【例6】（2020·定远县育才学校

）某科技股份有限公司为激励创新，计划逐年增加研发资金投入，若该公司2016年全年投入的研发资金为100万元，在此基础上，每年投入的研发资金比上一年增长10%，则该公司全年投入的研发奖金开始超过200万元的年份是（参考数据：lg1.10.041,lg20.301）A．202

2年B．2023年C．2024年D．2025年【答案】C【解析】设从2016年后，第n年该公司全年投入的研发资金开始超过200万元，由题意可得：100110%200n，即1.12n，两边取对数可得：lg20.3017.3lg1.10.041n，则8n，即该公司

全年投入的研发奖金开始超过200万元的年份是2024年.故选C.【一隅三反】1．（2020·湖北郧阳·高二月考）一种药在病人血液中的量保持1500mg以上才有效，而低于500mg病人就有危险．现给某病人注射了这种药2500mg，如果药在血液中以每小时20%的比例衰减，为了充分

发挥药物的利用价值，那么从现在起经过（）小时向病人的血液补充这种药，才能保持疗效．（附：1g20.301，1g30.4771，答案采取四舍五入精确到0.1h）A．2.3小时B．3.5小时C．5.6小时D．8.8小时【答案】A【解析】

设从现在起经过x小时向病人的血液补充这种药，才能保持疗效．则25000.81500x，0.80.6x，lg0.8lg0.6x，lg0.8lg0.6x，6lglg0.6lg2lg310.3010.47

711102.38lg0.83lg2130.3011lg10x．故选：A．2．（2020·重庆）某品牌牛奶的保质期y（单位：天）与储存温度x（单位：C）满足函数关系0,1k

xbyaaa.该品牌牛奶在0C的保质期为270天，在8C的保质期为180天，则该品牌牛奶在24C的保质期是（）A．60天B．70天C．80天D．90天【答案】C【解析】由题意可知，0270ba，8180kba，可

得8823kbkbaaa，所以332482270803kbkbaaa，故该品牌牛奶在24C的保质期是80天.故选：C3．（2020·黑龙江萨尔图·大庆实验中学）十三届全国人大一次会

议《政府工作报告》指出：过去五年来，我国经济实力跃上新台阶．国内生产总值从54万亿元增加到82.7万亿元，年均增长7.1%，占世界经济比重从11.4%提高到15%左右，对世界经济增长贡献率超过30%，2018年发展的预期目标是国内生产总值增长6.

5%左右．如果从2018年开始，以后每年的国内生产总值都按6.5%的增长率增长，那么2020年的国内生产总值约为（）（提示：31.0651.208）A．93.8万亿元B．97万亿元C．99.9万亿元D．106

.39万亿元【答案】C【解析】依题意可得2020年的国内生产总值约为382.716.5%82.71.20899.901699.9故选：C4．（2020·辽宁锦州）水葫芦原产于巴西，1901年作为观赏植物引入中国.现在南方一些水域水葫芦已泛滥

成灾严重影响航道安全和水生动物生长.某科研团队在某水域放入一定量水葫芦进行研究，发现其蔓延速度越来越快，经过2个月其覆盖面积为218m，经过3个月其覆盖面积为227m.现水葫芦覆盖面积y（单位2m）与经过时间()xxN个月的关系有两个函数模型(0,1)

xykaka与12(0)ypxqp可供选择.（参考数据：21.414,31.732,lg20.3010,lg30.4771）（Ⅰ）试判断哪个函数模型更合适，并求出该模型的解析式；（Ⅱ）

求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的1000倍.【答案】（1）38()()2xyxN（2）原先投放的水葫芦的面积为8m2,约经过17个月该水域中水葫芦面积是当初投放的1000倍.【解析】（Ⅰ）(0,1)xykaka的增长速度越来越快，12(0)ypxqp

的增长速度越来越慢.(0,1)xykaka依题意应选函数则有23=18=27kaka，解得3=2=8ak382xyxN，（Ⅱ）当0x时，8y该经过x个月该水域中水葫芦面积

是当初投放的1000倍.有38810002x32log1000xlg10003lg23lg3lg217.03答：原先投放的水葫芦的面积为8m2,约经过17个月该水域中水葫芦面积是当初投放的1000倍.