【文档说明】2021年高中数学人教版必修第一册：4.1《指数的运算》精品讲义(含解析).doc，共(9)页，510.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31230.html

以下为本文档部分文字说明：

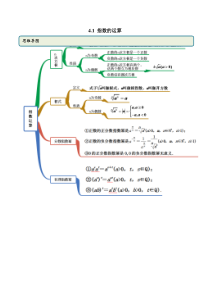
4.1指数的运算思维导图常见考法考点一根式的运算【例1】（2020·全国高一课时练习）化简下列各式：（1）22(53)(52)；（2）22(1)(3)(1)xxx…；（3）526526.【答案】（1）1（2）原式2,13,24,3.xxx„…（3）23

【解析】（1）原式|53||52|35521.（2）原式|1||3|xx，当13x时，原式132xx；当3x时，原式1324xxx.∴原式2,13,24,3.xxx

„…（3）原式2222(3)26(2)(3)26(2)22(32)(32)|32||32|323223.【一隅三反】1．（2020·全国高一课时练习）求下列各式的值：（1）322322

；（2）526642743.【答案】（1）22（2）22【解析】（1）原式2222(2)221(2)221(21)(21).212122；（2）原式222(32)(22)(2

3).32(22)2322.2．（2019·四川遂宁.高一期末）下列各式正确的是（）A．88aaB．01aC．44(4)4D．55()【答案】D【解析】对于A，

88aa，当a为负数时等式不成立，故A不正确；对于B，01a，当0a时无意义，故B不正确；对于C，44(4)4，左边为正，右边为负，故C不正确；对于D，55()，故D正确.故选：D.3．（2020·全国高一课时练习）若33x，则化简222169xxxx

________.【答案】22,314,13xxx【解析】因为2222216913xxxxxx所以，当31x时，原式1322xxx；当13x时，原式134xx

.将式子化简成含绝对值的式子，再对绝对值内的数进行正负讨论，去绝对值故答案为：22,314,13xxx考点二分数指数幂的运算【例2】（2020·全国高一课时练习）化简下列各式(0,0)ab；（1）33

22111143422()abababab；（2）2131121322ababbaba.【答案】（1）6ab（2）6a【解析】（1）原式11223233101381716132232361111442342abaababb

ab.（2）原式23221113171111132221623662222211322()ababaaababaabaabbb.【一

隅三反】1．（2020·全国高一课时练习）将下列根式化成分数指数幂的形式.（1）13·aa(a>0)；（2）252310xxx；（3）23243b(b>0).【答案】（1）512a；（2）35x；（3）1

9b.【解析】（1）原式＝1132·aa＝56a＝1526a＝512a.1.先把根式化成分数指数幂，然后利用指数幂的运算法则求解即可2.所求根式含有多重根号时，要搞清被开方数，由里向外用分数指数幂写出，然后用性质进行化简.（2）原式

＝23251·()xx＝4351·xx＝9351x＝91531()x＝351x＝35x.（3）原式＝[2134()b]23＝212()343b＝19b.2．（2020·全国高一课时练习）将下列根式化成分数指数幂的形式.（1）13·aa(a>0)；（2）22531(0)()xxx

；（3）23243b(b>0).【答案】（1）512(0)aa；（2）35(0)xx；（3）19(0)bb.【解析】（1）111111533322212··()(0)aaaaaaa；（2）3591422533535111(0)()()xxxxxxx

；（3）23212143639()(0)bbbb.考点三条件等式求值【例3】（2020·浙江高一课时练习）已知11223aa，求下列各式的值：（1）1aa.（2）22aa.（3）22332223aaaa.【答案】（1）7；（2）47；（

3）3.【解析】（1）将11223aa两边平方，得129aa，即17aa.（2）将上式两边平方，可得22249aa，∴2247aa.（3）∵3333111111122222222aaaaaaaaaa

1313(71)18aa，而2247aa，∴原式47245318315.【一隅三反】1．（2020·浙江高一课时练习）已知22335xx，那么1133xx等于（）A．7B．7C．7D．7【答案】C【解

析】当0x时，130x，130x，此时11330xx；当0x时，130x，130x，此时11330xx.2112233332527xxxx，因此，11337xx.故选：C.2．（2018·全国

高一期末）若11223xx,则332222x32xxx_____.【答案】13【解析】因为11223xx，所以平方得111129,?7,xxxx再平方得2222249,?47,xxxx

而3311112222x()13618xxxxx，因此33222231831.24723xxxx考点四综合运算【例4】（2020·浙江高一课时练习）计算下列各式：（1）1

0220.531222(0.01)54.（2）20.53207103720.12392748.本题考查指数幂的化简计算，涉及整体代换思想的应用，解题时要观察变量指数之间的倍数关系，结合完

全平方公式进行计算，但同时也要注意确定所求代数式的符号（3）011430.753237(0.064)(2)16|0.01|8.【答案】（1）1615；（2）100；（3）14380.【解析】（1）原式11221411116114910061015

.（2）原式122322516437390.127485937100310031648.（3）原式1430.41(2)20.1

10111143141681080.【一隅三反】1．（2020·云南寻甸.昆明黄冈实验学校高一月考4160.250343216(23)(22)4()28(2009)49；【答案】100【解析】4160.250343216(23)(22)4()28(2009)49

4131111126230322444(23)224()22(2009)74311233034447423(2)422(2009)108272

1100；2（2020·浙江高一课时练习）化简：3216842111111111111222222_______

_.【答案】63122【解析】原式432168211111111111111222222223216824

2111111111111222222232164481111111111222222

32168811111111222223216161111112222323211112226411

2263122.