【文档说明】2021年高中数学人教版必修第一册：1.3《集合的基本运算》精品讲义(含解析).doc，共(10)页，646.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31186.html

以下为本文档部分文字说明：

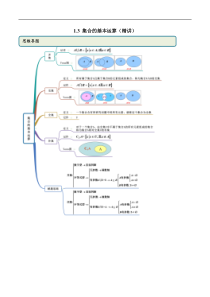
1.3集合的基本运算（精讲）思维导图常见考法考点一交集【例1】（1）（2020·上海高一开学考试）设集合A3,5,6,8，集合B4,5,7,8，则AB等于（）A．5,8B．3,,6C．4,7D．3,5,6,8（2）（2020·安徽省庐江金牛中学）已知集

合|12Mxx，|13Nxx，则MN（）A．1,3B．1,2C．1,2D．2,3【答案】（1）A（2）C【解析】（1）集合A3,5,6,8，集合B4,5,7,8，又集合A与集合

B中的公共元素为5,8，5,8AB，故选A.（2）集合|12Mxx，|13Nxx|121,2MNxx.故选：C.【一隅三反】1．（2020·全国高一课时练习）设集合2{|430}Axxx，{|230}Bx

x，则AB（）A．3(3,)2B．3(3,)2C．3(1,)2D．3(,3)21.交集：两个集合的相同部分的元素所组成的集合2.单个数字交集找相同，不等式的交集画数轴，不同集合高度画不同。【答案】D【解析】集合|130|13Axxxxx

，集合，所以3|32ABxx,故选D.2（2020·浙江省兰溪市第三中学高三开学考试）已知集合2{|560}Axxx，{|15}BxZx，则AB（）A．[2,3]B．(1,5

)C．2,3D．{2,3,4}【答案】C【解析】2560(2)(3)023xxxxx，23Axx，又{|15}2,3,4BxZx，所以2,3AB，故本题选C.3．（2020·湖南怀化高

二期末）设集合2|340AxZxx，|21Bxx，则AB（）A．{1,0,1,2}B．[1,2)C．{1,0,1}D．[1,2]【答案】A【解析】由题意得，2|340|141,0,1,2,3,4AxZxxxZx

，|21|3Bxxxx，则1,0,1,2,3,4|31,0,1,2ABxx，故选：A．考法二并集【例2】（2020·甘肃城关.兰大附中高三月考（理））

若集合22Axx，13Bxx，则AB（）A．2,3B．1,2C．2,2D．2,3【答案】D【解析】因为22Axx，13Bxx，

所以AB2,3.故选：D.【一隅三反】1．（2020·贵州南明贵阳一中高三其他（理））已知集合{22}Axx∣，若ABA，则B可能是（）A．1,1B．2,3C．1,3D．2,1【答案

】A【解析】因为ABA，所以BA，四个选项中只有1,1是集合A的子集.故选：A2（2020·上海高一课时练习）满足条件1,31,3,5A的所有集合A的个数是()A．1B．2C．3D．4【答案】D【解析】因为1,31,3,

5A，所以，集合A可能为5,1,5,5,3,1,3,5，即所有集合A的个数是4，故选D.3．（2019·浙江高一期中）已知集合2{|1}Pxx，2{|0}Qxxx，那么PQU=()A．{1,1}B．{1}C．{1,0,1}D．{0,1

}【答案】C【解析】因为2{|1}{1,1}Pxx，2{|0}{0,1}Qxxx，所以1,0,1PQ，故选：C考法三补集与全集【例3】（2020·上海高一课时练习）已知全集U={1,3,5,7,9},集合A={1,|a-5|,9},∁UA={5,7},则a的值

是()A．2B．8C．-2或8D．2或8【答案】D【解析】由由已知得5382aa或；故选D并集：两个集合所有元素集中在一起的集合，但是重复元素只写一次，要满足集合中的互异性【一隅三反】1．（2020·全国高一）设集合0,1,2,3U，集合2|0AxUxmx，若1,

2UCA，则实数m_____.【答案】-3【解析】因为集合0,1,2,3U，1,2UCA，A={0,3}，故m=-3.2．（2020·全国高一专题练习）已知全集2{2,3,23},1,2,3U

UaaAaCAa,则a的值为__________【答案】2【解析】由补集概念及集合中元素互异性知a应满足22222233(1)323|1|23(2)|1|3232(3)232233(4)2123433aaaaaaaaAaaBaaaaaa

或分两种情况进行讨论：在A中，由（1）得a=0依次代入（2）、（3）、（4）检验，不合②，故舍去．在B中，由（1）得a=－3,a=2，分别代入（2、（3）、（4）检验，a=－3不合②，故舍去，a=2能满足②③④，故a=2符合题意

．答案为：23．（2019·上海虹口.上外附中高一期中）设全集22,3,3Uaa，集合,3Aa，2UCA，则a=___________.【答案】3【解析】由2UCA,22,3,3Uaa可知23,3

Aaa,即23,3,3aaa.故232,3aaaa.当0a时,233aaaa,当0a时,23aaa即2230130aaaa,故3a.不满足2,3a.故3a.故答案为：3易错点：并不是所有的全集都是

用字母U表示，也不是都是R，要看题目的。考法四集合运算综合运用【例4】（2020·全国高一课时练习）已知集合3|0|31xMxNxxx，，则集合|1xx＝（）A．MNB．MNC．RMNðD．RMNð【答案】D【解析】301xx，解之得，31

x，则(,1)MN.故选：D.【一隅三反】1．（2019·浙江高三月考）已知集合{|(3)(1)0}Axxx，{1|1}Bxx‖，则RCAB（）A．[1,0)(2,3]B．(2,3]C．(,0)(2,)D．(1,0)(2,3)

【答案】A【解析】因为集合{|(3)(1)0}Axxx，{1|1}Bxx‖，所以{|3Axx或1}x，{|2Bxx或0}x，所以{|13}RCAxx，所以RCAB{|23xx

或10}x，故选A.2．（2020·浙江高三月考）已知全集1,0,1,2,3,4U，集合|1,AxxxN，1,3B，则UBAð（）A．4B．2,4C．1,2,4D．1,0

,2,4【答案】C【解析】因为|1,AxxxN，1,3B，所以0,1,3AB，则1,2,4UABð.故选：C.3．（2019·浙江高三月考）已知全集0,1,2,3,4,5,6U，集合0,1,3,5A，2,3,6B，则U

ABð多种集合运算的计算，先算括号内再算括号外，括号外的从左到右计算。（）A．3B．0,1,3,4C．0,1,3,4,5D．0,1,2,3,5,6【答案】C【解析】全集0,1,2,3,4,5,6U，集合2,3,6B，则0,1,4

,5UBð，又集合0,1,3,5A，因此，0,1,3,4,5UABð.故选：C.考法五求参数【例5】2．（2020·黑龙江萨尔图.大庆实验中学高二月考（理））已知集合2|3210Axxx

，|23Bxaxa，若AB，则实数a的取值范围是（）A．101,,32B．101,,32C．1,2,6

D．1,2,6【答案】B【解析】21|321013Axxxxx，当B时，32aa，解得3a，符合题意；当B时，2123aaa

或13323aaa，解得132a或103a，综上所述，实数a的取值范围是101,,32.故选：B【一隅三反】1．（2020·安徽金安六安一中高一期末（理））若不等式组2142xaxa的解集非空，

则实数a的取值范围是（）作为子集的集合，要分该集合是空集、不是空集两类讨论。A．1,3B．(,1)(3,)C．3,1D．(,3)(1,)【答案】A【解析】由题意2124xaxa，∴2124aa，即2230aa

，解得13a．故选：A．2（2020·湖北高一期末）设全集UR，已知集合3Axx或9x，集合Bxxa.若UCAB，则a的取值范围为（）A．3aB．3aC．9aD．9a【答案】C【解析】∵3Axx或9x，∴9|3UCAxx

，若UCAB，则9a，故选：C．3．（2020·浙江高一课时练习）设集合2320Axxx，222150Bxxaxa．（1）若2AB，求实数a的值；（2）若ABA，求实数a的取值范

围；（3）若全集UR，UABAð，求实数a的取值范围．【答案】（1）1或3（2）3aa（3）1,3,13,13aaaaa【解析】（1）由2320xx得1,2A，因为2AB，所以2B，所以244150aa

，整理得2430aa，解得1a或3．当1a时，2402,2Bxx，满足2AB；当3a时，24402Bxxx，满足2AB；故a的值为1或3．（2）由题意，知

1,2A．由ABA，得BA．当集合B时，关于x的方程222150xaxa没有实数根，所以2241450aa，即30a，解得3a．当集合B时，若集合B中只有一个元素，则2241450aa，整理得30a

，解得3a，此时24402Bxxx，符合题意；若集合B中有两个元素，则1,2B，所以22220430aaaa，无解．综上，可知实数a的取值范围为3aa．（3

）由UABAð，可知AB，所以221215044150aaaa，所以131313aaaa且且．综上，实数a的取值范围为1,3,13,13aaaaa．故

得解.