【文档说明】2021年高中数学人教版必修第一册：4.2《指数函数》精讲(含解析).doc，共(16)页，1004.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31161.html

以下为本文档部分文字说明：

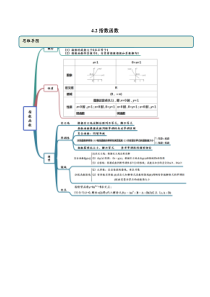
4.2指数函数思维导图常见考法考点一指数函数的判断【例1-1】（2019·河北桥西.邢台一中高一月考）下列函数中指数函数的个数是（）①23xy②13xy③3xy④21xya（a为常数，12a，1a）⑤3yx⑥4xy⑦4xyA．1B．2C．3D．4【答案】B【解

析】对①：指数式的系数为2，不是1，故不是指数函数；对②：其指数为1x，不是x，故不是指数函数；对③④：满足指数函数的定义，故都是指数函数；对⑤：是幂函数，不是指数函数；对⑥：指数式的系数为-1，不是1，故不是指数函数；对⑦：指数的底数为-4，不满足底数大于零且不为1的要求，故不是；综上

，是指数函数的只有③④，故选：B.【例1-2】（2019·河南中原.郑州一中高一开学考试）函数f(x)=(a2﹣3a+3)ax是指数函数，则a的值为（）A．1B．3C．2D．1或3【答案】C【解析】因为函数f(x)=(a2﹣3a+3)ax是指数函数，故可得2331aa解得1a或2a

，当1a时，不是指数函数，舍去.故选：C.【一隅三反】1．（2019·山东高三学业考试）函数2xyaa是指数函数，则（）A．1a或3aB．1aC．3aD．0a且1a【答案】C【解析】因为函数

2xyaa是指数函数所以21a，0a且1a，解得3a.故选：C.2．（2019·呼和浩特开来中学高一期中）若函数1()(3)2xfxaa是指数函数,则1()2f的值为()A．2B．-2C．22D．22【答案】D【解析】∵函数f（x）＝（1

2a﹣3）•ax是指数函数，∴12a﹣3＝1，a＞0，a≠1，解得a＝8，∴f（x）＝8x，∴f（12）822，故选：D．3．（2019·辽宁葫芦岛.高一月考）下列函数不是指数函数的是（）A．12xy

B．3xyC．4xyD．32xy【答案】A【解析】指数函数是形如xya（0a且1a）的函数.对于A：1222xxy，系数不是1，所以不是指数函数；对于B：133xxy，符

合指数函数的定义，所以是指数函数；对于C：4xy，符合指数函数的定义，所以是指数函数；对于D：382xxy，符合指数函数的定义，所以是指数函数.故选：A.考点二定义域和值域【例2-1】（2020·全国高一课时练习）求下列函数的定义域和值域：只有形

如(0,1)xyaaa的函数才是指数函数，系数等于1（1）142xy；（2）23xy；（3）22312xxy.【答案】（1）定义域{|4}xx，值域为{|0yy且1}

y；（2）定义域{|0}xx，值域{|1}yy；（3）定义域R，值域0,16【解析】（1）要使函数式有意义，则40x，解得4x.所以函数142xy的定义域为{|4}xx.因为104x，所以1421x，即函数142xy的值域为{|01}yyy，且.（2）要使

函数式有意义，则||0x…，解得0x，所以函数23xy的定义域为{|0}xx.因为0x，所以022133x，即函数23xy的值域为{|1}yy.（3）函数的定义域为R.因为2223(1)44xxx

，所以2234111622xx„.又223102xx，所以函数22312xxy的值域为0,16.【例2-2】（2018·湖南开福.长沙一中高一月考）若函数421xxya的值域为

[0，+∞），则实数a的取值范围是_____．【答案】（﹣∞，﹣2]【解析】设()421xxgxa，若函数421xxya的值域为[0，)，则等价于[0，)是()gx值域的子集，2()421(2)21xxxxgxaa，设

2xt，则0t，则2()1yhttat，(0)10h，当对称轴02at„，即0a…时，不满足条件．当02at，即0a时，则判别式△240a…，即022aaa或厔，则2a„，即实数a的取值范围是(，2

].故答案为：(，2]【一隅三反】1．（2020·全国高一课时练习）求下列函数的定义域和值域；（1）12xy；（2）12xy；（3）2xy.【答案】（1）定义域为R，值域为(0,)；（2

）(,0]，[0,1)；（3）[0,)，[1,).【解析】（1）12xy的定义域为R，值域为(0,).（2）由120x知0x„，故12xy的定义域为(,0]；由0121x„知0121x„，故12xy的值域为[0,

1).（3）2xy的定义域为[0,)；由0x…知21x…，故2xy的值域为[1,).2．（2020·全国高一课时练习）求下列函数的定义域与值域.（1）112xy（2）1(0,1xxayaa且1)a（3）110.3;xy（4

）513.xy【答案】（1）定义域为[0,)；值域为[0,1)；（2）定义域为R；值域为(－1，1)；（3）定义域为{1}xx∣；值域为{0yy∣且1}y；（4）定义域为15xx∣；值域为{1}yy∣.1.对于y＝af(x)这类函数，

①定义域是指使f(x)有意义的x的取值范围．②值域问题，应分以下两步求解：ⅰ由定义域求出u＝f(x)的值域；ⅱ利用指数函数y＝au的单调性或利用图象求得此函数的值域．2.对于y＝(ax)2＋b·ax＋c这类函数，①定义域是R.②值域可以分以

下两步求解：ⅰ设t＝ax，求出t的范围；ⅱ利用二次函数y＝t2＋bt＋c的配方法求函数的值域．【解析】（1）1102x，解得：0x，∴原函数的定义域为[0,)，令11(0)2xtx，则01,01tt∴原函数的值域为[0,1)（2）

原函数的定义域为R.设xat，则(0,)t，11221111ttyttt，0,11tt，1201,2011tt，21111t，即原函数的值域为(1,1).（3）由10

x得1x，所以函数定义域为{|1}xx，由101x得1y，所以函数值域为{|0yy且1}y.(4)由510x得15x，所以函数定义域为15xx∣，由510x得1y，所以函数值域为{1}

yy∣.3．（2020·河北新华.石家庄二中高二期末）若函数1,121,14xxxfxax的值域为,a，则a的取值范围为（）A．1,4B．11,4

2C．1,12D．1,14【答案】B【解析】当1x时，1,212xfx当1x时，114,4xfxaaa函数fx的值域为,a11421

2aa，即11,42a故选：B4．（2020·云南五华.昆明一中高三其他（理））设函数211yx的定义域为A，函数12xy的值域为B，则AB()A．0,1B．0,1C．1,1D．1,1【答案】A【

解析】函数定义域满足：210x，即11x，所以11Axx，函数12xy的值域0Byy，所以0,1AB，故选：A.5．（2019·湖南高一期中）若函数2411()3axxfx有最大值3，则实数a

的值为（）A．2B．1C．1D．2【答案】D【解析】由于函数2411()3axxfx有最大值3，所以0a，且当422xaa时，fx取得最大值为2224411412113333aaa

aafa，故4411,2,2aaa.故选：D考点三指数函数性质【例3】（1）（2020·贵溪市实验中学高二期末（文））若函数6(3)

3,7(),7xaxxfxax单调递增,则实数a的取值范围是()A．9,34B．9,34C．1,3D．2,3（2）（2019·湖南岳阳楼.岳阳一中高一期中）已知函数1()2xfx，则不等式24(3)faf

a的解集为()A．(4,1)B．(1,4)C．(1,4)D．(0,4)（3）（2019·湖北襄阳）如果1111222ba，那么（）A．abaaabB．aababaC．baa

aabD．baaaba【答案】（1）B（2）B(3)C【解析】（1）函数6(3)3,7(),7xaxxfxax„单调递增，301373aaaa解得934a所以实数

a的取值范围是9,34．故选：B．（2）可知函数()fx为减函数，由2(4)(3)fafa，可得243aa，整理得2340aa，解得14a，所以不等式的解集为(1,4)．故选B.(3)根据函数1()2xfx在R是减函数，且1111222b

a，所以10ba，所以aababa，故选C.【一隅三反】1．（2019·浙江南湖.嘉兴一中高一月考）函数2213xxy为增函数的区间是（）A．1,B．,1

C．1,D．,111.指数函数性质记忆口诀指数增减要看清，抓住底数不放松；反正底数大于0，不等于1已表明；底数若是大于1，图象从下往上增；底数0到1之间，图象从上往下减；无论函数增和减，图象都过(0,1)点．2.比较幂值大小的三种类型及处理方法【

答案】C【解析】∵13uy是减函数，222(1)1uxxx在(,1]上递增，在[1,)上递减，∴函数2213xxy的增区间是[1,)．故选：C．2．（2019·浙江柯城.衢州二中高三一模）已知定义在R上的函数

||32xmfxm为实数）为偶函数，记0.2log3af，5logbfe，cfm，则()A．cbaB．cabC．acbD．abc【答案】B【解析】()fx为偶函数，()()fxfx，||||3232xmxm，|

|||xmxm；0m；||()32xfx；()fx在[0，)上单调递减，并且0.25(|log3|)(log3)aff，5(log)bfe，()()cfmf550

loglog3ecab．故选：B．3．（2020·浙江高一课时练习）设0.914y，0.4828y，1.5312y，则（）A．312yyyB．213yyyC．123yyyD．132yyy【答案

】D【解析】1.50.920.91.80.4830.481.441.35121422,22282,yyy，因为函数2xy在定义域上为单调递增函数，所以132yyy．故选：D．4．（2020·永安市第三中学高二月考）

若关于x的方程94340xxa有解，则实数a的取值范围是（）A．(,8][0,)B．,4C．[8,4)D．(,8]【答案】D【解析】由9(4)340xxa，得443(4)0,(4)343

3xxxxaa（当且仅当32x时等号成立），解得8a故选D5（2020·上海高一课时练习）已知函数2221()2xxfx，则该函数的单调递增区间是_________

_.【答案】(,1]【解析】由题得函数的定义域为R.设2122,()2uuxxv，函数222,uxx在(-,-1]单调递减，在[1,)单调递增，函数1()2uv在其定义域内单调递减，所以2221()2xxfx在

(-,-1]单调递增，在[1,)单调递减.故答案为：(,1].6．（2020·上海普陀.曹杨二中高一期末）函数12xy的单调递增区间为________【答案】(,0]【解析】函数12,010221,1xxxyxx

，根据指数函数单调性可得，函数在(,0]单调递增，在()0,+?单调递减，所以函数12xy的单调递增区间为(,0].故答案为：(,0]7．（2020·全国高一课时练习）比较下列各题中的两个值的大小．（1）0.

10.8，0.21.25；（2）1，1；（3）30.2，0.23.【答案】（1）0.10.20.81.25（2）11（3）0.230.23【解析】（1）因为0.10.10.1450.854

，0.20.251.254，又指数函数54xy为增函数，且0.10.2，所以0.10.25544，即0.10.20.81.25.（2）1

01，（3）30.200.21，10.2553330，所以0.230.23.考点四定点【例4】（2020·浙江高一课时练习）函数xfxa（0a，且1a）的图象过定点P，则P点的坐标为（）A．(1,

5)B．(1,4)C．(0,5)D．(0,4)【答案】A【解析】因为xya的图象恒过(0,1)点，则1xya的图象恒过(1,1)点，所以xfxa恒过定点1,5P.故选A.【一隅三反】1．（2019·涡阳县第九中学高二期末）函数10,1xyaaa

的图象必经过点（）A．(0,1)B．(1,1)C．0,2D．(2,2)【答案】C【解析】函数xya的图象过点(0,1)，而函数1xya的图象是把函数xya的图象向上平移1个单位，函数1xya的图象必经过的点(0,2)．故选

：C．2．（2019·贵州省织金县第二中学高一期中）函数21()xfxa(0a且1)a过定点（）A．(1,1)B．1(,0)2C．(1,0)D．1(,1)2【答案】D【解析】令12102xx，所以函数21()xfxa(0a且1)a过定点1

(,1)2．3．（2020·宁夏贺兰县景博中学高一月考）函数y=ax﹣1+2（a＞0且a≠1）图象一定过点（）A．（1，1）B．（1，3）C．（2，0）D．（4，0）【答案】B由x﹣1=0，解得x=1，此时y=1+

2=3，即函数的图象过定点（1，3），故选B考点五图像【例5-1】（2020·广东顺德一中高一期中）函数1(0,1)xyaaaa的图像可能是（）．A．B．C．D．【答案】D【解析】∵0a，∴10a，

∴函数xya需向下平移1a个单位，不过（0,1）点，所以排除A，当1a时，∴101a，所以排除B，当01a时，∴11a，所以排除C，故选D.【例5-2】（2020·浙江高一课时练习）若函数(01,1)xyaaam的图像在第一、

三、四象限内，则（）A．1aB．1a，且0mC．01a，且0mD．01a【答案】B【解析】因为函数xya的图像在第一、二象限内，所以欲使其图像在第三、四象限内，必须将xya向下移动，因为当01a时，图像向下移动，只能经过第一、

二、四象限或第二、三、四象限，所以只有当1a时，图像向下移动才可能经过第一、三、四象限，故1a，因为图像向下移动小于一个单位时，图像经过第一、二、三象限，而向下移动一个单位时，图像恰好经过原点和第一、三象限，所以欲使

图像经过第一、三、四象限，则必须向下平移超过一个单位，故11m，0m，故选：B.【一隅三反】1．（2019·浙江高一期中）函数yxa与xya，其中0a，且1a，它们的大致图象在同一直角坐标系中有可能是()A．B．C．D．【答案】D【解析】因为函数yxa单调递增，所

以排除AC选项；当1a时，yxa与y轴交点纵坐标大于1，函数xya单调递增，B选项错误；当01a时，yxa与y轴交点纵坐标大于0小于1，函数xya单调递减；D选项正确.故选：D2．（2020·全国高

一课时练习）在如图所示的图象中，二次函数2yaxbxc与函数xbya的图象可能是（）A．B．C．D．【答案】A【解析】根据选项中二次函数图象，可知0c=，根据选项中指数函数的图象，

可知01ba，所以1022ba，所以二次函数2yaxbxc的对称轴在y轴左侧，且1,022bxa，所以可排除B、C、D，只有A符合题意.故选：A.3．（2020·上海高一课

时练习）若函数2xym的图像不经过第二象限，则m的取值范围是()A．m1B．1mC．1mD．1m【答案】D【解析】指数函数2xy过点()0,1,则函数2xym过点0,1m,若图像不经过第二象限,则10m,即1m,故选

：D4．（2020·内蒙古集宁一中高二期末（理））若直线2ya与函数|1|(0,1)xyaaa的图象有两个公共点，则a的取值范围是___________【答案】102，【解析】当01,1

aa时，做出|1|xya图象，如下图所示，直线2ya与函数|1|(0,1)xyaaa的图象有两个公共点时，1021,02aa.故答案为:102，