【文档说明】2021年高中数学人教版必修第一册：5.5《三角恒等变换》精品讲义(原卷版).doc，共(8)页，564.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-31043.html

以下为本文档部分文字说明：

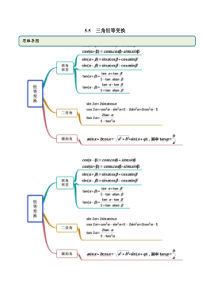
5.5三角恒等变换思维导图考点一两角和差公式【例1】（1）（2020·湖北茅箭·十堰一中月考）cos80sin40sin50cos10的值为（）A．12B．22C．32D．32（2）（2020·海南枫叶国际学校高一

期中）cos20cos10sin20sin10=（）A．sin10B．cos10C．12D．32（3）（2020·四川成都·高一期末）求值：tan25tan353tan25tan35（）

A．23B．33C．1D．3（4）（2020·山西应县一中高一期中（文））22cos15sin19522的值为（）A．32B．12C．32D．12常见考法【一隅三反】1．（2020·安徽蚌埠·高一期末）求值：cos75c

os45sin75sin45（）A．12B．32C．12D．322．（2020·镇原中学高一期末）求值：（1）tan10tan503tan10tan50；（2）3tan1513tan15.3．（202

0·湖南娄底·高一期末）下列化简正确的是（）A．1cos82sin52sin82cos522B．1sin15sin30sin754C．tan48tan7231tan48tan72D．223cos15sin152考点二给值求值【例2】（1）（202

0·商丘市第一高级中学高一期末）已知5cos5，,02，则tan4（）A．13B．3C．13D．13（2）（2020·湖南娄星·娄底一中高一期末）已知为锐角，且3cos

()65，则sin（）A．43310B．43310C．33410D．33410（3）（2020·河南林州一中高一月考）若02，2，1cos43，3cos423，则cos2（）A．539B．53

9C．33D．33【一隅三反】1．（2020·山东聊城·高一期末）角的终边与单位圆的交点坐标为31(,)22，将的终边绕原点顺时针旋转34，得到角，则cos()（）A．624B．624C．

314D．02．（2020·江西省铜鼓中学高一期末）已知3tan5，π1tan42，则πtan4的值为（）A．17B．113C．1113D．1173．（2020·阜新市第二高级中学高一期末）已知3312,

,,sin,sin45413，则cos4__________．考点三给值求角给值(式)求值的策略(1)当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式．(2)当“已知角”

有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，然后应用诱导公式把“所求角”变成“已知角”．【例3】（2020·辽宁沈阳·高一期中）已知为锐角，为钝角且25cos5，tan3，则的值为（）A．34B．23

C．3D．4【一隅三反】1．（2020·全国高三其他（理））已知sinsinsina，若3，且0,，则（）A．23B．2C．3D．62．（2020·湖北东西湖·华中师大一附中高一

月考）若1cos7，53sin14，02，02，则角的值为（）A．4B．3C．8D．63．（2020·江西省铜鼓中学高一期末）已知43sin7，,2.（1）求2sin2的值；（2）若33sin()14a，0,2

，求的值.考点四二倍角先求出问题角的三角函数值，再根据角的范围求出角【例4】（1）（2020·宁夏原州·固原一中高三其他（文））若3sin()5，则cos2（）A．2425B．725C．725D．2425（2）（2020·全国专题练习（文））计算：

55coscoscoscos12121212（）A．32B．12C．12D．32（3）（2020·赤峰二中高三三模（理））已知角α的终边经过点(-4,-3)，则cos(2)2

（）A．2425B．1225C．1225D．2425【一隅三反】1．（2020·吴起高级中学高一期末）已知角α的终边经过点P（﹣3，1），则cos2α＝（）A．35B．35C．45D．452．（2020·山西其他（理））已知12cossin6

，则tan2（）A．43B．32C．84359D．03．（2020·四川金牛·成都外国语学校高一开学考试（理））设1sin44，则sin2（）A．78B．18C．18D．784．（2020·湖南省岳阳县第一中学高三月考）已知α为锐角，

5sin25，则cos2＝（）A．45B．35-C．35D．45考点五角的拼凑【例5】（1）（2020·湖北蔡甸·汉阳一中高三其他（理））若1sin()33，则cos(2)3A．79B．23C．23D．79（2）（2020·湖南娄底·高一期末）已知2co

s()63，则5cos(2)3的值为（）A．59B．19C．19D．59【一隅三反】1．（2020·安徽高二期末（理））已知1sin35，则sin26

（）A．225B．2325C．225D．23252．（2020·全国高三其他（理））已知为第三象限角，且2sin22cos2，则πsin24的值为（）A．710B．710C．7210D．72103．（2020·全国高三其他（文））设43sin

cos65，则cos23（）A．5725B．5725C．725D．725考点六恒等变化【例6】（1）（2020·安徽相山·淮北一中月考（理））12cos502tan50（）A．1B

．12C．32D．22（2）（2020·山西应县一中高一期中（理））22cos51sin40cos40的值为（）A．-1B．-2C．1D．2【一隅三反】1．（2020·海原县第一中学高一期末）计算：31

cos10sin170的结果是（）A．-4B．-2C．2D．42．（2018·福建高二期末（文））sin65sin35cos30cos35__________.3．（2020·全国专题练习（理））1cos201sin10tan52sin20tan5

_______.三角函数式化简的常用方法：(1)异角化同角：善于发现角之间的差别与联系，合理对角拆分，恰当选择三角公式，能求值的求出值，减少角的个数；(2)异名化同名：统一三角函数名称，利用诱导公式切弦互化、二倍角公式等实

现名称的统一；(3)异次化同次：统一三角函数的次数，一般利用降幂公式化高次为低次．