【文档说明】《“两边成比例且夹角相等”》教学设计1-九年级下册数学苏科版.doc，共(3)页，105.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-26309.html

以下为本文档部分文字说明：

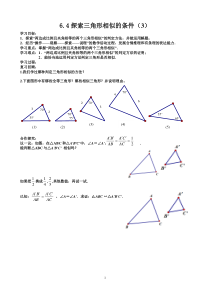
16.4探索三角形相似的条件（3）学习目标：1．探索“两边成比例且夹角相等的两个三角形相似”的判定方法，并能运用解题；2．经历“操作——观察——探索——说理”的数学活动过程，发展合情推理和有条理的表达能力．学习重点：掌握“两边成比例且夹角相等的两个三角形

相似”．学习难点：1．“两边成比例且夹角相等的两个三角形相似”的判定方法的证明；2．能恰当地运用判定方法判定三角形是否相似．学习过程：复习回顾：1.我们学过哪种判定三角形相似的方法？2.下面图形中有哪些全等三角形？哪些相似

三角形？并说明理由。35°2370°75°70°70°326470°65°35°合作探究：议一议：如图，在△ABC和△A'B'C'中，∠A＝∠A'，．能判断△ABC与△A'B'C'相似吗？如果把21换成41,32,其他数值，再试一试．已知：ACCAABBA''''，∠A＝∠A'．求证：

△ABC∽△A'B'C'．12ABACABAC(1)(2)(3)(5)(4)2探索三角形相似的条件：两边_________________________的两个三角形相似．应用新知：1、当BE=时，△ABE∽△CDE.324EDCBA2、如图，∠1=∠2，要使△ABC∽△ADE，还需

要添加的条件是___________（只需添加一个条件）.21EDCBA3、如图，在△ABC中，D在AB上，要说明△ACD∽△ABC相似，已经具备了条件，还需添加的条件是，或或。ABCD符号语言：3例题讲解例1如图，点D在△ABC

内，点E在△ABC外，∠1=∠2，∠3=∠4.△DBE与△ABC相似吗？为什么？EDCB4312A小试牛刀：如图，在正方形ABCD中，点M、N分别在AB、BC上，AB＝4，AM＝1，BN＝0.75，（1）△ADM与△BMN相似吗？为什么？（2）求∠DMN的度数；DABCMN拓展延伸

1.如图，在△ABC中，AB=4，AC=2.(1)当AD=时，使△ACD∽△ABC.DCBA(2)当AE=时，使△AEB∽△ABC.(3)此时，BE与DC有怎样的位置关系？为什么？DEBCA小结：课堂作业：