【文档说明】《函数的应用》导学案-九年级下册数学北京版.docx，共(5)页，518.883 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-25572.html

以下为本文档部分文字说明：

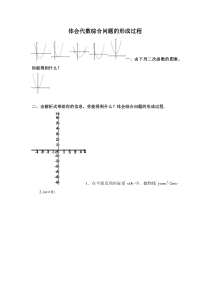
体会代数综合问题的形成过程一、由下列二次函数的图象，你能得到什么？二、由解析式带给你的信息，你能得到什么？体会综合问题的形成过程.1．在平面直角坐标系xOy中，抛物线y=mx2-2mx-2(m≠0)2.在平面直角坐标系xOy中，抛物线三、作业1．平面

直角坐标系xOy中，抛物线交y轴于A点，交直线x=4于B点．（1）抛物线的对称轴为x=（用含m的代数式表示）；（2）若AB∥x轴，求抛物线的表达式；（3）记抛物线在A，B之间的部分为图象G（包含A，B两点），若对于图象G上任意一点P（，），，求m的取值

范围．（2017海淀一模）2．在平面直角坐标系中，抛物线经过点（0，），（3，4）．（1）求抛物线的表达式及对称轴；（2）设点关于原点的对称点为，点是抛物线对称轴上一动点，记抛物线在，之间的部分为图象

（包含，两点）．若直线与图象有公共点，结合函数图像，求点纵坐标的取值范围．(2014)3.在平面直角坐标系中，抛物线与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，(1)直接写出抛物线的对称轴及点C的坐标.

(2)若AB=4，求抛物线的表达式及顶点坐标.(3)若点P(-1,1)，点Q(4,1)连接PQ，若抛物线与线段PQ有两个公共点时，求m的取值范围.