【文档说明】《总结与复习》导学案-九年级上册数学北京版.doc，共(5)页，79.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-25530.html

以下为本文档部分文字说明：

1圆中的“双垂图”学案一、复习已知：如图，在△ABC中，∠ACB=90°，CD⊥AB（1）相等的锐角∠A=，∠B=.（2）线段之间的一些数量关系AC•BC=，AC2=，BC2=，CD2=.DCBA二、引例：已知：如上图，在△ABC中，∠ACB=90°，CD⊥AB.（1）若AC=8,BC

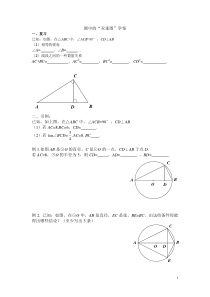
=6，CD=.（2）若tan∠BCD=43,AC=8,BC.例1.如图AB是⊙O的直径，C是⊙O的一点，CD⊥AB于点D.若AC=8，⊙O的半径为5，则CD=，AD=，BD=.例2.已知：如图，在⊙O中，AB是直径，EC是弦，BE=BC，由这些条件你能

得出哪些结论？（至少写出5条）OCBADEDOCBA2例3.如图，△ABC内接于⊙O，AB是直径，BD与⊙O相切于点B，与AC延长线交于D，∠A=30°，BC=32.（1）你能求出图中哪些线段的长？（2）过点C作弦CF⊥AB于E，交⊙O于F，求

CF的.4.变式提升：已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=43．（1）求⊙O的半径长；（2）求线段CF长．OFEDCBAODCBA35如图

，AB是⊙O的直径，C是弧AB的中点，⊙O的切线BD交AC的延长线于点D，E是OB的中点，CE的延长线交切线DB于点F，AF交⊙O于点H，连结BH．（1）求证：AC=CD；（2）若OB=2，求BH的长．6已知，如图，BC

是以线段AB为直径的⊙O的切线，AC交⊙O于点D，过点D作弦DE⊥AB垂足为点F，连接BE、BD（1）若∠A=30°，CD＝3，求⊙O的半径r.（2）若AD=12，BD=5，求DE的长.FECDBOAOHFEDCBA4如图，AB为⊙O的直径，弦CD⊥AB于点H，过点B

作⊙O的切线与AD的延长线交于F．（1）求证：ABCF（2）若sinC=35，DF=6，求⊙O的半径．.如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE.（1）求证：DE与⊙O相切.（2）若tanC=25，DE=2，求AD的长．如图

，在△ABC中，AB=AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点，DFAC于F．（1）求证：DF为⊙O的切线；（2）若3cos5C，CF=9，求AE的长．如图，AB是⊙O的直径，点E是弧BD上一点，∠DAC=∠AED．（1）求证

：AC是⊙O的切线；ODECBAOFEABCDHOFDCBA5（2）若点E是弧BD的中点，连结AE交BC于点F，当BD=5，CD=4时，求DF的值．