【文档说明】《19.6 反比例函数的图象、性质、应用》PPT课件3-九年级上册数学北京版.ppt，共(16)页，1.963 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-23721.html

以下为本文档部分文字说明：

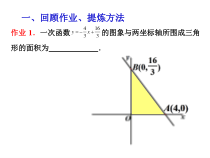
一、回顾作业、提炼方法作业1．一次函数41633yx的图象与两坐标轴所围成三角形的面积为．作业2.如图，直线362yx与x轴相交于点A,直线33yx与x轴相交于点B,两直线相交于点C，则ABC的面积为．D作业3．如图，

一次函数122yx的图象上有两点(1,),(3,)AmBn，直线AB与x轴交于点P，AC⊥x轴于C，BD⊥x轴于D，则梯形ACBD的面积为．122yx31,273,2作业4．如图，点P(m,n)是双曲线4yx上一点，经过点P分别向x轴、y轴作垂线段，则矩

形OAPB的面积为；连接OP，则OBP的面积为；OAP的面积为．问题：若把改为该题的结果是怎样的呢？4yx(0)kykx(m,n)P(m,n)D(m,n)一次函数与反比例函数中的面积问题二、割补转化、巧求面积例1.如图，反比例函数4yx在第一象限的图象上有两点A(

1，m)、B(3，n)．求△AOB的面积．443,3B43,3B问题：如何添加辅助线，将△ABC转化为容易求得面积的图形呢？学生活动：1.独立思考2分钟（先不用计算结果）2.组内交流3分钟（看哪个小组转化的方法多）三、割补转化、巧求面积BBEFBAE

F2,3A（）4,0C（）0,2D（）61B（，）四、反思小结、凝炼提升主要解决了哪些问题？一体会了哪些数学思想方法？二四、反思小结、凝炼提升数形结合思想转化思想五、布置作业、延续探究