【文档说明】《回顾与反思》教学设计3-八年级上册数学冀教版.doc，共(2)页，83.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-22686.html

以下为本文档部分文字说明：

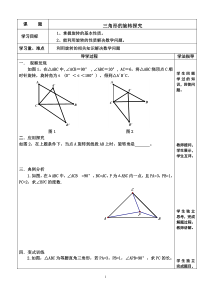
1课题三角形的旋转探究学习目标1、掌握旋转的基本性质。2、能利用旋转的性质解决数学问题。学习重、难点利用旋转的相关知识解决数学问题导学过程学法指导一．观察发现如图1，在△ABC中,∠ACB＝90°,∠ABC＝30°,AC＝6，将△ABC绕顶点C顺时针旋

转，旋转角为α(0°＜α＜180°)，得到△A´B´C．CBAA'B'ACBB'A'图1图2二．应用探究如图2，在上题条件下，当点A旋转到线段AB上时，旋转角是。三．典例分析1.如图，在ΔABC中，∠ACB=90°，BC=AC，P为

ΔABC内一点，且PA=3，PB=1，PC=2，求∠BPC的度数.BCAP四．变式训练2.如图，△ABC为等腰直角三角形，若PA=3，PB=1，∠APB=90°，求PC的长。学生回顾学过的知识，回答问题。教师提问，学生展示，学生互评。学生独立思考，

完成解题过程。教师讲解。学生独立完成题目，2BCAP四．归纳总结直击中考1．如图1，正方形OABC的两边OA、OC分别在x、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°,则旋转后点D的对应点D′的坐标是。2.如图，在△ABC中，AB=2，AC=4，将△ABC绕点

C按逆时针方向旋转得到△A′B′C，使CB′∥AB，分别延长AB，CA′相交于点D，则线段BD的长为．3.如图3，在Rt△ABC中，D为斜边AB上的一点，AD=2，BD=1，且四边形DECF是正方形，则阴影部分的面积是。图1图2图

3展示解题过程，学生互评。自我训练