【文档说明】《有关圆的典型例题的解析》教学设计3-九年级上册数学青岛版.doc，共(2)页，65.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-22269.html

以下为本文档部分文字说明：

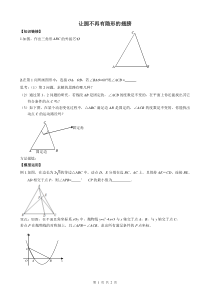
第1页共2页让圆不再有隐形的翅膀【知识链接】1.如图，作出三角形ABC的外接⊙O2.在第1问所画图形中，连接OA，OB，若∠BAO=60°则∠ACB=.思考：（1）第2问题，求解的思路有哪几种？（2）通过第1、2问题的研究，若线段AB是固定的，∠ACB的度数是不变的，在平面上你还能找出其它符合条件

的点C吗？（3）如下图，在某个动态变化过程中，△ABC满足边AB是固定的，∠ACB的度数是不变的，你能找出动点C的运动路径吗？方法提炼：【模型运用】例1.如图，在边长为23的等边△ABC中，动点D、E分别在边BC、AC上，且

保持AE＝CD，连接BE、AD相交于点P，则∠APB=°CP的最小值为．变式：如图，在平面直角坐标系xOy中，抛物线y=x²-4x+3与x轴交于点A，B，与y轴交于点C，若点P在抛物线的对称轴上，且∠APB＝∠AC

B，求出所有满足条件的P点坐标．ABCABC固定边固定角OABxyC第2页共2页【自主探究】问题提出：如图，已知：线段AB，试在平面内找到符合所有条件的点C，使∠ACB＝30°.思路点拨：（1）点C的运动路径是什么？（2）确

定路径的关键是什么？（3）你的思路有哪些？方法提炼：自主探索1：在平面直角坐标系中，已知点A(3，0)、B(－1，0)，点C是y轴上的一个动点，当∠BCA＝45°时，点C的坐标为.自主探索2：在平面直角坐标系中，已知点A(3，0)、B(－1，0)，点

C是y轴上的一个动点，当∠BCA＝135°时，点C的坐标为.变式：如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使∠APB＝30°，则满足条件的点P的个数是__________．【课堂小结

】（1）本节课的学习后，你原有的知识框架中，又增加了什么数学模型？（2）此类模型，对于我们解决哪些数学问题是有帮助的？（3）在运用此类模型时，你感觉有哪些注意点？【拓展练习】如图，已抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A(1，0)、B(4，0)两点，与y轴交于

C(0，2)，连结AC、BC．（1）求抛物线解析式；（2）BC的垂直平分线交抛物线于D、E两点，求直线DE的解析式；（3）若点P在抛物线的对称轴上，且∠CPB＝∠CAB，求出所有满足条件的P点坐标．OABxyCABlC