【文档说明】《用直角三角形解实际中的方位角、坡角问题》PPT课件2-九年级上册数学沪科版.ppt，共(24)页，907.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-20265.html

以下为本文档部分文字说明：

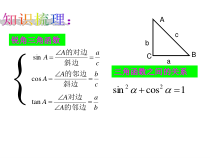
ABCabc锐角三角函数caAA斜边的对边sincbAA斜边的邻边cosbaAAA的邻边对边tan三角函数之间的关系1cossin22学科网特殊角三角函数值角度函数030045060sincostan

2122232322213313角度逐渐增大的值sin的值cos的值tan知识链接：（1）2sin30°+3tan30°+tan45°(2)+tan60°cos30°2．在△ABC中，∠C＝90°，tanA＝则

sinB＝()311023310...103410ACDD3213332121＝解原式＝0245cos223322)2(2＝解原式＝Z.x.

x.K1.计算：3．在正方形网格中，如图2所示，则∠B正弦值为（）1233...2223ACDB三边关系：；三角关系：；边角关系：sinA＝cosB＝，cosA＝sinB＝，tanA＝，(2)直角三角形可解的条件和解法条件：解直角三角

形时知道其中的2个元素(至少有一个是边)，就可以求出其余的3个未知元素．a2＋b2＝c2∠A＝90°－∠Bacbc解直角三角形的依据(1)在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B,∠C的对边．ab解直角三角形①知一边一锐角，先由锐角关系求出另一锐角；知斜边，再用正弦(

或余弦)求另两边；知直角边用正切求另一直角边，再用正弦或勾股定理求斜边．②知两边：先用勾股定理求另一边，再用边角关系求锐角．③斜三角形问题可通过添加适当的辅助线转化为直角三角形问题．解法：例1.科技改变生活，手机导航极大地方便了人们的出行，如图，小明一家自驾到古镇游

玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶4千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B、C两地的距离．解：如解图，过点B作BD⊥AC于点D，在Rt△A

BD中，AB＝4千米，sin∠A＝，∴BD＝AB·sinA＝4×＝2(千米)，在Rt△BCD中，∠C＝45°，sin∠C＝，∴BC＝＝＝2(千米)．答：B、C两地的距离为2千米．BDAB323sinBDC232266BDBC若三角形内角中有已知角时，则通过作该三角形的高

，将原三角形分为两个直角三角形求解，且公共边是解题的关键，常考关系式BC＝BD＋CD.模型分析练习1.为加快城乡对接，建设全域美丽乡村，某地区对A、B两地间的公路进行改建．如图，A、B两地之间有一座山．汽车原来从A

地到B地需途径C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶．已知BC＝80千米，∠A＝45°，∠B＝30°.(1)开通隧道前，汽车从A地到B地大约要走多少千米？(2)开通隧道后，汽车从A地到B地大约可以少走多少千米？(结果精确到0.1千米)(参考数据：≈1.41，≈1.73

)23解：(1)如解图，过C作CD⊥AB于点D，在Rt△BCD中，∵BC＝80千米，∠B＝30°，∴DC＝BC·sin30°＝40千米，在Rt△ACD中，∵∠A＝45°，∴AD＝CD＝40千米，AC＝40千米，∴AC＋BC＝40＋80≈136.4千米；答：开通

隧道前，汽车从A地到B地大约走136.4千米；(2)在Rt△BCD中，∵BC＝80，∠B＝30°，∴BD＝BC·cos30°＝40，∴AB＝AD＋BD＝40＋40≈109.2，136．4－109.2＝27.2，答：开通隧道后汽车从A

地到B地大约可以少走27.2千米.2233例2.黄河，既是一条源远流长、波澜壮阔的自然河，又是一条孕育中华民族灿烂文明的母亲河，数学课外实践活动中，小林和同学们在黄河南岸小路上的A，B两点处，用测角仪分别对北岸的观景亭D进行测量．如图，测得∠DAC

＝45°，∠DBC＝65°.若AB＝200米，求观景亭D到小路AC的距离约为多少米？(结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14)解：如解图，过点D作DE⊥AC，垂足为E，设BE＝x米，在

Rt△DEB中，tan∠DBE＝.∵∠DBC＝65°，∴DE＝x·tan65°，又∵∠DAC＝45°，∴AE＝DE，∴200＋x＝x·tan65°，解得x≈175.4，∴DE＝200＋x≈375(米)．答：观景亭D到小

路AC的距离约为375米．DEBE若三角形中有已知角，可在三角形外作高，构造有公共直角的两三角形求解，且求出公共边是解题的关键，常考关系式AD＝AC－DC模型分析练习2：如图，某商场为方便顾客使用购物车，准备将滚动电梯的坡面倾斜角由45°降为30°，如果改动前电梯的坡面A

B长为12米，点D、B、C在同一水平面上，AD⊥CD，求改动后电梯水平宽度增加部分BC的长．(结果精确到0.1米，参考数据：≈1.41，≈1.73，≈2.45)236解：由题意得，在Rt△ABD中，∵

∠ABD＝45°，AB＝12米，∴BD＝AD＝6米，在Rt△ACD中，∠C＝30°，∴CD＝＝6(米)，∴BC＝CD－BD＝6－6≈6.2(米)．答：改动后电梯水平宽度增加部分BC的长约为6.2米．233AD662过较短的底AB作直角梯形的高BE，构造一个矩形和直角三角形，常考关系式DC＝DE＋

EC＝DE＋AB.模型分析例3：如图，电线杆CD上的C处引拉线CE，CF固定电线杆，在离电线杆6米的B处安置测角仪(点B，E，D在同一直线上)，在A处测得电线杆上C处的仰角为30°，已知测角仪的高AB＝1.5米，BE＝2.3米，

求拉线CE的长，(精确到0.1米，参考数据≈1.41，≈1.73)．第8题图32解：如解图，过点A作AM⊥CD于点M，则四边形ABDM为矩形，AM＝BD＝6米，在Rt△ACM中，∵∠CAM＝30°，AM＝6米，∴CM＝AM·tan∠CAM＝6×＝2(米)，∴C

D＝2＋1.5≈4.96(米)，在Rt△CDE中，ED＝6－2.3＝3.7(米)，∴CE＝≈6.2(米)，∴拉线CE长约6.2米．333322DECD练习3：如图，测量人员在山脚A处测得山顶B的仰角为45°，沿着仰角为30°的

山坡前进1000米到达D处，在D处测得山顶B的仰角为60°，BC⊥AC，求山的高度BC.解：∵∠BAC＝45°，∠DAC＝30°，∴∠BAD＝15°，∵∠BDE＝60°，∠BED＝90°，∴∠DBE＝30°，∵∠ABC＝45°，∴∠ABD＝15°，∴∠ABD＝∠DAB，∴AD＝

BD＝1000米，如解图，过点D作DF⊥AC于点F，∵AC⊥BC，DF⊥AC，DE⊥BC，∴∠DFC＝∠ACB＝∠DEC＝90°∴四边形DFCE是矩形，∴DF＝CE在Rt△ADF中，∵∠DAF＝30°，∴DF＝AD＝500(米)，∴EC＝DF＝500米，BE＝100

0·sin60°＝500(米)．∴BC＝EC＋BE＝500＋500(米)，山的高度BC为(500＋500)米.33123tanAaAAb的对边的邻边sinAaAc的对边斜边cosAbAc的

邻边斜边sinBbBc的对边斜边cosBaBc的邻边斜边tanBbBBa的对边的邻边ABCbac复习小结解应用题时，先要将实际问题转化为数学问题，找出直角三角形并寻找联系已知条件和未知量的桥梁，从而利用解直角三角形的知识

得到数学问题的答案，最后得到符合实际情况的答案．解直角三角形的一般思路是：有斜(斜边)用弦(正弦、余弦)，无斜用切(正切)，宁乘勿除，取原避中．对于较复杂的图形，要善于将其分解成简单的图形，并借助桥梁(相等的边、公共

边、相等的角等)的作用将两个图形有机地联系在一起，从而达到解题的目的．作业：《解直角三角形》专题训练