【文档说明】《相似三角形的综合应用》教学设计1-九年级上册数学沪科版.doc，共(5)页，330.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-20210.html

以下为本文档部分文字说明：

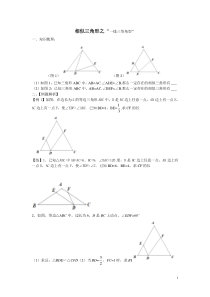
1相似三角形之“一线三等角型”一、知识梳理：（图1）（图2）（1）如图1：已知三角形ABC中，AB=AC,∠ADE=∠B,那么一定存在的相似三角形有___（2）如图2：已知三角形ABC中，AB=AC,∠

DEF=∠B,那么一定存在的相似三角形有___二、【例题解析】【例1】如图，在边长为2的等边三角形ABC中，D是BC边上任意一点，AB边上有一点E，AC边上有一点F，使∠EDF=∠ABC.已知BD=1，BE=31,求CF

的长【练】1、已知△ABC中AB=AC=6、BC=8，∠BAC=120度，D是BC边上任意一点，AB边上有一点E，AC边上有一点F，使∠EDF=∠C.已知BD=6、BE=4，求:CF的长2、如图，等边

△ABC中，边长为6，D是BC上动点，∠EDF=60°（1）求证：△BDE∽△CFD（2）当BD=23，FC=1时，求BE2【例2】在ABC中，OBCACC,3,4,90o是AB上的一点，且52ABAO，点P是AC上的一个动点，OPPQ交线段BC于点Q

，（不与点B,C重合），已知AP=2，求CQ【练】在直角三角形ABC中，DBCABC,,90o是AB边上的一点，E是在AC边上的一个动点，（与A,C不重合），DFDEDF,与射线BC相交于点F.(1)、当点D是边AB

的中点时，求证：DFDE(2)、当mDBAD，求DFDE的值【例3】已知在等腰三角形ABC中，AB=AC,D是BC的中点，∠EDF=∠B,求证：△BDE∽△DFE.【练】在边长为4的等边ABC中，D是BC的中点，点E、F分别在AB、AC上（点D不与点C、点B重合），且保持ABCEDF

,连接EF.(1)已知BE=1,DF=2.求DE的值(2)求∠BED=∠DEF3【例4】如图，已知边长为3的等边ABC，点F在边BC上，1CF，点E是射线BA上一动点，以线段EF为边向右侧作等边EFG，直

线,EGFG交直线AC于点,MN，（1）写出图中与BEF相似的三角形；（2）证明其中一对三角形相似；（3）设,BExMNy，求y与x之间的函数关系式，并写出自变量x的取值范围；【练】如图，在△ABC中，8ACAB，10BC，D是BC边上的一个动点，点E在AC边上，且CA

DE．(1)求证：△ABD∽△DCE；(2)如果xBD，yAE，求y与x的函数解析式，并写出自变量x的定义域；(3)当点D是BC的中点时，试说明△ADE是什么三角形，并说明理由．【例5】已知在梯形ABCD中，AD∥B

C，AD＜BC，且AD＝5，AB＝DC＝2．（1）如图8，P为AD上的一点，满足过点D作DG⊥EF于点G，∠BPC＝∠A．①求证；△ABP∽△DPC②求AP的长．4【练】如图，在梯形ABCD中，AD∥BC，6

ABCDBC，3AD．点M为边BC的中点，以M为顶点作EMFB，射线ME交腰AB于点E，射线MF交腰CD于点F，联结EF．（1）求证：△MEF∽△BEM；（2）若△BEM是以BM为腰的等腰三角形，求EF的长；（3）若EFCD，求

BE的长．【家庭作业】1、如图，在ABC中，90C，6AC，43BCAC，D是BC边的中点，E为AB边上的一个动点，作90DEF，EF交射线BC于点F．设BEx，BED的面积为y．（1）求y关于x的函数关系式，并写出自变量x的取值

范围；（2）如果以B、E、F为顶点的三角形与BED相似，求BED的面积.2、如图，已知在△ABC中，AB=AC=6，BC=5，D是AB上一点，BD=2，E是BC上一动点，联结DE，并作DEFB，射线EF交线段AC于F．（1）求证：△DBE∽

△ECF；（2）当F是线段AC中点时，求线段BE的长；5（3）联结DF，如果△DEF与△DBE相似，求FC的长．3、已知在梯形ABCD中，AD∥BC，AD＜BC，且BC=6，AB=DC=4，点E是AB的中点．（1）如图，P为BC上的一点，且BP=2．求

证：△BEP∽△CPD；（2）如果点P在BC边上移动（点P与点B、C不重合），且满足∠EPF=∠C，PF交直线CD于点F，同时交直线AD于点M，那么①当点F在线段CD的延长线上时，设BP=x，DF=y，求y关于x的函数解析式，并写出函数的定义域；②当BEPDMFSS

49时，求BP的长