【文档说明】《17.4 一元二次方程的根与系数的关系》PPT课件3-八年级下册数学沪科版.ppt，共(13)页，1.102 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-20134.html

以下为本文档部分文字说明：

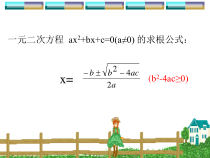
一元二次方程ax2+bx+c=0(a≠0)的求根公式：x=aacbb242(b2-4ac≥0)17.4一元二次方程的根与系数的关系解下列方程并完成填空：方程两根两根和X1+x2两根积x1x2x1x2x2-7x+12=0x2+3x-4=03x

2-4x+1=02x2+3x-2=0341271-3-4-4-1--221233431131方程两根两根和X1+x2两根积x1x2x1x2x2-7x+12=0x2+3x-4=03x2-4x+1=02x2+3x-2=0-341271-3-4-4-1-221233134311若一

元二次方程ax2+bx+c=0(a≠0)的两根为x1、x2,则21xx.21xx.abacaacbbx2421aacbbx2422X1+x2=aacbb242aacbb242+=ab22=ab-X1x2=aacbb242aacb

b242●=242)42(2)(aacbb=244aac=ac证明：设ax2+bx+c=0(a≠0)的两根为x1、x2,则一元二次方程的根与系数的关系：如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2,那么x1+x2=

,x1x2=ab-ac在使用根与系数的关系时，应注意：⑴不是一般式的要先化成一般式；⑵在使用X1+X2=－时，注意“－”不要漏写。ab如果方程x2+px+q=0的两根是X1，X2，那么X1+X2=,X1X2=.－Pq一元二次方程根与系数的关系是法国数学家“

韦达”发现的,所以我们又称之为韦达定理.1、说出下列各方程的两根之和与两根之积：(1)x2-2x-1=0(3)2x2-6x=0(4)3x2=4(2)2x2-3x+=021x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2=-2341342、方程2

x2-3x+1=0的两根记作x1,x2，不解方程，求：;2111xx)1)(1(21xx212xx21xx411412则：21xx2221xx221)(xx＝221)(xx221)(xx214xx＝几种常见的求值:2111.1xx2121xxx

x)1)(1.(221xx1)(2121xxxx2122122212)(.3xxxxxx212212214)().(4xxxxxx1.一元二次方程根与系数的关系？acabacbxax

xxxxxx2121212.;,)0(0则有的两根分别是如果小结：2.几种常见的求值4、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值.拓展练习