【文档说明】《一次函数的图像与性质》PPT课件3-八年级上册数学沪科版.ppt，共(17)页，3.221 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-20022.html

以下为本文档部分文字说明：

02-yx12-yxxy212xy一次函数的图像和性质（复习课）（1）理解一次函数和正比例函数的意义；（2）能根据已知条件确定一次函数表达式；（3）会利用待定系数法确定一次函数的解析式；（4）能画出一次函数的图像，根据一次函数表

达式探索函数的图像和性质。理解了解掌握运用（1）一次函数的意义；（了解）（2）一次函数的表达式；（掌握）（3）利用待定系数法确定一次函数的表达式；（掌握）（4）一次函数的图像和性质；（掌握）（5）正比例函数；（理解）（6）一次函数不二元一次方程的关系；（理解

）（7）用一次函数解决问题。（运用）2019年安徽省中考考试大纲考查目标2016-2018年安徽中考题分析2019年中考命题预测年份考察点题型题号分值2018一次函数与反比例函数的综合填空题135一次函数表达式的确定解答题22（1）52

017一次函数的图像与性质与二次函数、反比例函数的图像与性质的综合选择题94一次函数表达式的确定解答题22（1）42016一次函数与反比例函数综合解答题2010“一次函数”在近3年安徽省中考题的分布情况一次函数的表达式、一次函数的图像和性质、应用一次函

数解决有关的实际问题，一般丌单独考察，往往不反比例函数、二次函数、一次方程组等综合考察。考察题型：选择题、填空题、解答题中都有可能出现，经常出现在解答题中，不其他知识综合考察。【中考趋势】预测2019年的安徽省中考仍会延续这种命题趋势，考察一次函数的图像和性质，也会不实际问题

相结合，考察实际问题不一次函数图像的结合，戒结合反比例函数戒二次函数考察一次函数表达式的确定等，以选择题不解答题为主。◇一次函数一般地,如果有y=kx+b(k,b为常数,且k≠0),那么y叫做x的一次函

数；◇正比例函数特别地,当b=0时,一次函数y=kx+b就成为y=kx(k为常数,k≠0),此时y叫做x的正比例函数。正比例函数是特殊的一次函数。◇截距我们把b叫做直线y=kx+b在y轴上的截距。（1）先设一次

函数关系式为y=kx+b（k、b是待确定的系数）；（2）代入两个条件，得到关于k、b的二元一次方程组；（3）求出k、b的值，再代回y=kx+b中即可。（8年4考）◇“待定系数法”求一次函数解析式的一般步骤：一次函数y=kx+b(k≠0）图像k、b的符号经过象限

增减性正比例函数y=kx(k≠0）图像xyobxyobxyobxyobk>0b>0k>0b<0k<0b>0k<0b<0一、二、三一、三、四一、二、四二、三、四y随x的增大而增大y随x的增大而减小xyoxyok____0１、图象是经过（０，）与（１，）的一条直线。２、当k

>0时，图象过_________象限；y随x的增大而增大。当k<0时，图象过_________象限；y随x的增大而减少。0k一、三二、四k____0＞＜1.一次函数图象的平移：左右平移:y=kx+b上下平移:y=kx+b【特别提醒】（1）一次函数图象

的平移中,左右平移改变x的取值,上下平移改变y的取值;（2）平移的规律可记为“左加右减,上加下减”。y=k(x-m)+by=kx+b+nxyoxyo1.两直线平行关系的结论：已知直线112221,::ykxbyllkb

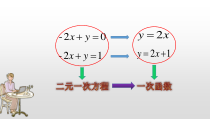
12,ll若∥则_____________;①1212,,kkbb若且≠则______。②。，2121bbkk12ll∥xyo1l2l利用一次函数的图象求二元一次方程组的近似解和丌等式的解

集。(1)任何一个二元一次方程组都可以化成两个一次函数的形式,作出相应的两个一次函数的图象,得到的交点的_______,就是这个二元一次方程组的解。(2)一次函数y=kx+b(k,b是常数,且k≠0)的图象位于x轴_______的部分对应的x的取值范围就是不等式kx+b>0的解集;同样,

其图象位于x轴下方的部分对应的x的取值范围就是不等式___________的解集。坐标上方kx+b<0一次函数的应用(8年5考)温馨提醒：利用函数的图象解方程组戒求丌等式的解集,都是从“形”的角度研究“数”问题,是“数形结合”思想的体现。小试身手1

、设正比例函数y=mx的图象经过点A（m，4），且y的值随x值的增大而减小，则m=（）A.2B.﹣2C.4D.-4B2.点A（5，y1）和B（2，y2）都在直线y=-x+1上，则y1与y2的关系是（）A、y1≥y2B、y1＝y2C、y1＜y2D、y1＞y2

C小试身手3.(2017年安徽第9题)已知抛物线y=ax2+bx+c与反比例函数的图象在第一象限有一个公共点,其横坐标为1.则一次函数y=bx+ac的图象可能是()byxB小试身手4.已知一次函数的图象与直线y＝－x＋1平行，且过点(8,2)，则此一次函数的解析式为______

________。y＝－x＋105.已知一次函数y＝bx＋5和y＝－x＋a的图象交于点P(1,2)，直接写出方程组y＋x＝a(bx－y＝－5，)的解为___________。12xy小试身手6.(2018年安徽第13题)如图,正比例函数y=kx与反比例函数的图象有一个交点A(2,m)，

AB⊥x轴于点B。平移直线y=kx使其经过点B,得到直线l.则直线l对应的函数表达式是_____________.xy6332yx小试身手7.如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上

平移2个单位得到点P2,点P2恰好在直线l上.(1)点P2的坐标为;(2)求直线l的函数表达式。(2)设直线l的函数表达式为y=mx+n(m≠0),P1(2,1),P2(3,3)代入y=mx+n，得2𝑚+𝑛=1,3𝑚+𝑛=3,解得𝑚=2,𝑛=-3,∴直线l的函数

表达式为y=2x-3。(3，3).