【文档说明】《阅读材料 有趣的拼图》导学案4-八年级下册数学浙教版.doc，共(3)页，71.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-18675.html

以下为本文档部分文字说明：

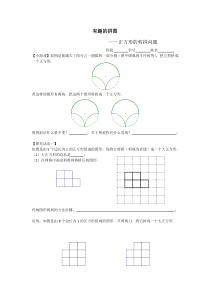
有趣的拼图——正方形的剪拼问题班级学号姓名【小游戏】如图是被减去了四分之一圆弧的一部分圆（图中圆弧的半径相等），把它剪拼成一个正方形；若这样的图形有两块，把这两个图形剪拼成一个正方形.剪拼前后什么量不变？；关于剪痕你有什么发现？；【探究活动一】如图是由5个边长为1的正方形组成的图形

，现将它剪拼（剪痕为直线）成一个大正方形.（1）大正方形的边长是；（2）在网格中画出剪痕和剪拼后的图形.归纳图形剪拼的方法步骤：；应用：如图是由8个边长为1的正方形组成的图形，只剪两刀，将它拼成一个大正方形.【探究活动二】如图，正方形ABCD的边CD在正方形ECGF的边CE上，B，C，G三

点在一条直线上，且边长分别为5和12.把这个图形剪拼成一个正方形.思考：如果正方形ABCD和正方形ECGF的边长都是任意的，其余条件不变，你还能把这样的图形剪拼成一个正方形吗？变式：如图，正方形ABCD的边长为12，等腰直角△AFE的斜边AE=10，且边AD和AE在同一直

线上.把这个图形剪拼成一个正方形.【课堂小结】19世纪，匈牙利数学家鲍耶证明了下述定理：任意给定两个面积相等的多边形，它们互相之间都可以通过剪拼得到.追溯历史，鲍耶运用的方法就是转化为基本图形来证明，从而解决问题，他分别解决了如下

问题：（1）任意一个三角形可以剪拼成一个矩形；（2）任意一个矩形可以剪拼成一个正方形；（3）任意两个正方形可以剪拼成一个大正方形；DACGEFBEFABDC想一想：边长没有数值怎么办；边长是任意的会出现哪些情况？请你画图试一试.（4）任意多个正方形可以剪拼成

一个大正方形；（5）任意一个多边形都可以剪拼成一个正方形.这节课，我们探究了一类把图形剪拼成正方形的问题，如果要剪拼成矩形、菱形或者其它图形，又该怎样剪拼，方法上是否有相通之处呢？关于图形的剪拼，你还想了解哪些内容，或者有哪些新的想法……请同学们课后查阅相关资料，探究更多图形剪拼的知识，设计一份

以图形的剪拼为主题的海报！