【文档说明】14.1.2《幂的乘方》PPT课件3-八年级上册数学人教版.ppt，共(20)页，1.726 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-17352.html

以下为本文档部分文字说明：

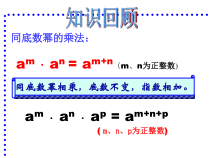
同底数幂的乘法：am·an=am+n(m、n为正整数)同底数幂相乘，底数不变，指数相加。am·an·ap=am+n+p(m、n、p为正整数)已知：am=2，an=3.求am+n=？.解：am+n=am·an=

2×3=6深入探索----议一议612aa6+a判断下面计算是否正确，如有错误请改正。(×)观察下面式子分别表示什么意义？(32)3(42)4(a2)5(am)3上面四个式子的底数分别是、、、.32a2am4214.1.2幂的乘

方⑴⑵⑶(m是正整数）根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:663m活动1(32)3=××=(3)()(a2)3=××=(a)()(am)3=××=(a)()323232a2a2a2amamam?)(nma对于任意底数a与任意正整数m,n,(am)n=amn(mn都

是正整数)即：幂的乘方，底数不变，指数相乘例1:计算:(1)(103)5;(2)(a4)4;(3)(am)2;(4)-(x4)3.解:(1)(103)5=103Χ5=1015(2)(a4)4=a4Χ4=a16(3)(am)2=amΧ2=a2m(4)-(x4)3

=-x4Χ3=-x12.下列各式对吗？请说出你的观点和理由：(1)(a4)3=a7()(2)a4a3=a12()(3)(a2)3+(a3)2=(a6)2()(4)(x3)2=x32=x9()××××活动2练一练(×)(×)我是法官我来判！a6·a4=a24(x3)3=x623()x

32（-x）(×)-(x2)3八年级数学=-x2×3=-x6;(-x2)3=-x2×3=-x6;-(x3)2=-x3×2=-x6;(-x3)2=x2×3=x6;【-(-x)3】²43])[((1)yx⑵(a-b)3［(a-

b)3］2⑶［(x-y)2］2［(y-x)2］31.计算：(1)-(xm)5;(2)(a2)3∙a5（3）(4)23)(y2（a2）6－（a3）42.计算：2342)((1)aaa.2423)()

)(2(xx.活动3探究1、【（32）3】42、【（a3）4】3解：1、【（32）3】4=（32×3）4=32×3×4=3242、【（a3）4】3=（a3×4）3=a3×4×3=a36则【（am）n】p=amnp变式563])([xmnnmmnaaa)()(幂的乘方法则的变

式活动4探究:2、(x6)2=(x2)6=填空：1、(103)4=(104)3=10121012x12x12(103)4=(104)3(x6)2=(x2)6变式幂的乘方的逆运算：(1)x13·x7=x（）=()5=()4=()10；(2)a2m=()2=()m（m为正整数）

.mnnmmnaaa)()(20x4x5x2ama21．(m2)3·m4等于()BA．m9B．m10C．m12D．m142．计算：(1)[(x＋y)2]6＝____________；(2)a8＋(a2)4＝________

____.2a83．已知x2n＝3，则(xn)4＝________.9点拔：(xn)4＝x4n＝(x2n)2＝32＝9.(x＋y)124.已知10a＝5,10b＝6，则102a＋103b的值为________241点拨：102a＋103b＝(10a)2＋(10b

)3＝52＋63＝241.课堂小结1.幂的乘方的法则nmnmaa)((m、n都是正整数）幂的乘方，底数不变，指数相乘.语言叙述符号叙述.2.幂的乘方的法则可以逆用.即nmmnaa)(mna)(3.多重乘方也具有这一性质.如pnmpnmaa])[(（其中m、n、p都是正

整数）公式中的a可表示一个数、字母、式子等.