【文档说明】12.2.2《“边角边”判定三角形全等》PPT课件10-八年级上册数学人教版.ppt，共(15)页，528.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-17288.html

以下为本文档部分文字说明：

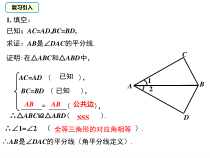
1.填空：已知：AC=AD,BC=BD,求证：AB是∠DAC的平分线.AC=AD()，BC=BD()，=()，∴△ABC≌△ABD().∴∠1=∠2（）.∴AB是∠DAC的平分线（角平分线定义）.ABCD12已知已知SSS证明:在△ABC和△AB

D中，ABAB公共边全等三角形的对应角相等复习引入12.2三角形全等的判定（2）已知三角形的两条边分别是10cm，18cm，且这两边的夹角是80°，画出这个三角形，把所画的三角形剪下来。问1：把你们所制作的三角形与小组的同伴所制作的三角形进行比较，观察

它们是不是全等？活动1问2：回顾作图过程，两个三角形全等已经满足了哪三个等量关系？猜想：两边和它们的夹角分别相等的两个三角形全等。问3：作图的结果反映了什么结论？请你尝试用文字语言概括出来？尺规作图：已知任意△ABC，画出一个△A′B′C′，使A′B′＝AB，A′C′＝AC，∠A′＝

∠A（即两边和它们的夹角分别相等）.画完后，将△A´B´C´放到∆ABC上，它们是否也会全等？猜想：两边和它们的夹角分别相等的两个三角形全等。作图验证探究ABCABCA′DEB′C′作法：（1）画∠DA'E=∠A；（2）在射线A'D上截取A'B'=AB,在射线A'E上

截取A'C'=AC；（3）连接B'C'.在△ABC和△A′B′C′中，∴△ABC≌△A′B′C′（SAS）文字语言：两边和它们的夹角分别相等的两个三角形全等（简写成“边角边”或“SAS”）．知识要点“边角边”判定方法几何语言：AB=A′B′，∠A=∠A′，AC=A′C′

，ABCA′B′C′SAS中的角必须是两边的“夹角”，书写时A必须放在中间的位置练习1：如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（）A、∠BCA=∠FB、∠A=∠EDFC、BC∥EFD、∠B=∠E练习2：如图，已知AB=AC，要

说明△ABD≌△ACE。若以“SAS”为依据，只能添加的一个条件是。DAD=AE练习3：如图，已知△ABC和△DCB中，AB=DC，请补充一个条件____________，使△ABC≌△DCB。思路：找夹角找第三边已知两边：AB=DC，BC=CB∠ABC=∠DCB（SAS）AC=

DB（SSS）ABCD小结：证明两个三角形全等，要结合题目的条件和结论，挖掘图形中的隐含条件，选择恰当的判定方法（SSS或SAS）例2如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B。连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使

CE＝CB．连接DE，那么量出DE的长就是A、B的距离，为什么?C·AEDB分析问题：AB=DE△ABC≌△DEC现有条件CA=CD,CB=CE图形隐含的条件∠1=∠2(SAS)12CA=CD，∠1=∠2，CB=

CE，解：在△ABC和△DEC，∴AB=DE.即DE的长就是A、B的距离。∠A=∠D∴AB∥DE问：线段AB与线段DE有什么位置关系？证明分别属于两个三角形的线段相等或者角相等的问题，常常通过证明这两个三角形全等来解决

．.归纳∴△ABC≌△DEC（SAS）1、如图，两车从南北方向的路段AB的A端出发，分别向东、向西行进相同的距离，到达C，D两地。此时C，D到B的距离相等吗？为什么？BDAC解：相等，理由如下：2、如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，求证：∠A=∠DADBEFC依题意

，得∠BAD=∠BAC=90°，AD=AC继续探讨三角形全等的条件：两边一角思考1：已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？ABCABC∠A是AB和AC的夹角边－角－边∠B

是AC边的对角边－边－角①两边及夹角分别相等的两个三角形全等（SAS)；②两边及其中一边的对角分别相等的两个三角形全等吗？用“两边一角”判定三角形全等时，这个角必须是两边的夹角想一想：如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC.固定住长木棍，转动短木

棍，得到△ABD.BACD有两边和其中一边的对角分别相等的两个三角形不一定全等.归纳△ABC和△ABD满足AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.两边和其中一边的对角分别相等思考2：两边及一角分别相等的

两个三角形全等吗？练习：下列条件中，不能证明△ABC≌△DEF的是()A．AB＝DE，∠B＝∠E，BC＝EFB．AB＝DE，∠A＝∠D，AC＝DFC．BC＝EF，∠B＝∠E，AC＝DFD．BC＝EF，∠C＝∠F，AC＝DFC课堂小结

边角边内容有两边及夹角分别相等的两个三角形全等（简写成“SAS”)应用为证明三角形全等提供了新的证法注意1.已知两边，则考虑找两边的“夹角”2.已知一角和这角的一夹边，则考虑找这角的另一夹边两边的夹角