【文档说明】24.3.2《正多边形的有关概念、正多边形与圆的关系》PPT课件-九年级上册数学部编版.ppt，共(26)页，1.238 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-17183.html

以下为本文档部分文字说明：

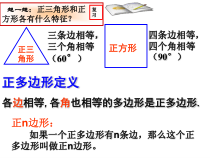
各边相等,各角也相等的多边形是正多边形.三条边相等，三个角相等（60°）四条边相等，四个角相等（90°）正三角形正方形正多边形定义想一想：正三角形和正方形各有什么特征？复习正n边形：如果一个正多边形有n条边，那么这个正多边形叫做正n边形。想

一想：菱形是正多边形吗？矩形呢?为什么？各边相等但各角不相等各角相等但各边不相等××找一找观察下列图形，从这些图形中找出相应的正多边形.3、正多边形都是图形。正多边形的性质及对称性4、边数是偶数的正多边形还是图形。1、正多边形的各边相等2、正多边形的各角相等想一想：正n边

形有条对称轴。轴对称中心对称n正n边形的每一个内角的度数都是____________;外角是___________;nn1802）（n360正多边形的计算正n边形的边长为a,它的周长是。na①正五边形的内角和为，每个内角的度数为。②若一个正多边形

的外角是30度，则这个正多边形是正边形。540度108度十二观察下列多边形的边数和形状，我发现。正六边形正八边形正十二边形正十七边形正n边形的边数越多,形状就越接近于圆人教版九年级（上）数学你知道了正多边形与圆的关

系吗？正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.·ABCDEOABCDE探索新知如图,把⊙O分成相等的6段弧,依次连接各分点得到正六边形ABCDEF.∴AB=BC=CD=DE=EF=FA,∴∠A=∠B.同理∠B=∠C

=∠D=∠E=∠F又∵六边形ABCDEF的顶点都在⊙O上,∴六边形ABCDEF是⊙O的内接正六边形,⊙O是六边形ABCDE的外接圆.我们以圆内接正六边形为例证明.∵AB=BC=CD=DE=EF=FA∴

BDF=CEA=4ABEFCD.ABO123ABCDE45归纳：如果将一个圆n等分，依次连接各分点得到一个n边形，这个n边形一定是正n边形弦相等（多边形的边相等）弧相等圆周角相等（多边形的角相等）→多边形是正多边形③正多边形每一边所对的圆心角叫做正多边形的中心角①我们把一个正多边形的

外接圆的圆心叫做这个正多边形的中心②外接圆的半径叫做正多边形的半径④中心到正多边形的一边的距离叫做正多边形的边心距O·ABCDEFM概念中心n360中心角想一想：正多边形的中心角和外角有什么关系？中心

角半径R边心距rEFCD.ABOMABAM21nnAOM1803602121中心角.RtΔ222AMOMOAAOM中，有在中心角一半边长一半半径R边心距rMCO探索新知设正n边形的边长为a,半径为R,边心距为r,它的周长为，面积为。454180436021214

中心角时，当AOMn探索新知边心距r半径R60OMCA边心距r半径R45OMCA边心距r半径R30MCOA603180336021213中心角时，当AOMn306180636021216中心角时，当AOMn如图，正六边形ABCDE

F的外接圆半径为4，求这个正六边形的中心角、边长、周长和面积各是多少？BA同步练习CDEFO●G智慧背囊：正多边形边长的一半、半径、边心距构成了一个直角三角形，正多边形的有关计算都可以化归到这个直角三角形中。有一个亭

子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解:如图由于ABCDEF是正六边形,所以它的中心角等于，△OBC是等边三角形，从而正六边形的边长等于它的半径.因此,亭子地基的周长l

=4×6=24(m).OABCDEFRPr实际运用360606利用勾股定理,可得边心距224223.r亭子地基的面积211242341.6(m).22Slr在Rt△OPB中,OB=4,PB=4222

BC，OABCDEFRPr例题讲解要用半径为8cm圆形木板截出一个正方形模具，则所截的正方形模具的边长最长应为_____________cm．活学活用1．正八边形的每个内角是______度.135°第一关2．如图，正六边形ABCDEF内接于⊙O，则∠CFD的度数是

（）A.60°B.45°C.30°D.22.5°C第二关3．已知正六边形的边心距为，则它的周长是_____.312第三关ABO4．如图，正六边形ABCDEF的半径为2，以它的中心O为坐标原点，顶点B、E在x轴上，求正六边形ABCDEF的各顶点的坐标．OFEDCBAxyA（-1，）3B（

-2，0）C（-1，）3D（1，）3E（2，0）F（1，）3第四关随堂作业A基础达标1、已知正三角形、正方形、正六边形的半径都是R，请你将各正多边形的边长、边心距、周长和面积值填在下表中．（用R来表示）2、圆内接正六边形一边所对的圆周角是（）（A）

30．（B）60．（C）150．（D）30或150．3、若一个正多边形的每个内角的度数是中心角的3倍，则正多边形的边数是（）（A）4．（B）6．（C）8．（D）12．边长边心距周长面积正三角形正方形正六边形随堂作业B感受中考4、如图，有一个边长为1.5cm的正六边形，如果要剪一张圆形

纸片完全盖住这个图形，那么这张圆形纸片的最小半径为___________cm．5、已知圆内接正六边形的边长是1，则这个圆的内接正方形的边长是____________．FEDCBA课后实践从正五角星形的内角谈起我们常见到的五

星红旗上的五角星形，不但给庄严的感觉，而且还给人一种和谐、对称、协调的美感，很容易得到它的一个内角为36．我们将圆周五等分，得五个分点1、2、3、4、5，如果按1→2→3→4→5相连，则得一个正五边形（如图①）．如果按1→3→5→2→4→1相连，则得一个正五角星形（如图②）．前者看成是5

/1边形，后者则可以看成是5/2边形．所以每一个内角为．图①图②图③图④以此类推，如图③、④将两个七角星形分别看成7/2边形和7/3边形，其内角分别为，．有兴趣的同学不妨继续沿着这个思路研究下去，你一定会有很大的收获．55180236227

754018022277718018023371.课本P107第1题323正多边形边数内角中心角半径边长边心距周长面积360°4161212033639

090228412060221263课后作业边心距r半径R60OMCA边心距r半径R30MCOA边心距r半径R45OMCA2．边长为6的正三角形的半径是________.32ABCDEFO3．如图，⊙O的周长为c

m,求以它的半径为边长的正六边形ABCDEF的面积．π62cm2327S课后作业