【文档说明】22.1.2《二次函数y=ax2的图像和性质》导学案-九年级上册数学部编版.doc，共(5)页，233.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-17066.html

以下为本文档部分文字说明：

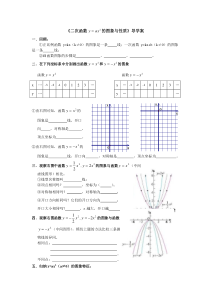
《二次函数2axy的图象与性质》导学案一．回顾：①正比例函数y=kx（k≠0）的图象是一条线；一次函数y=kx+b（k≠0）的图象是一条线；②画函数图象的步骤是、、。二．在下列坐标系中分别画出函数2xy和

2xy的图象函数2xy函数2xy①由右图可知，函数2xy的图象是线，开口向，对称轴是，顶点坐标为。②由右图可知，函数2xy的图象是线，开口向，对称轴是，顶点坐标为。三．观察右图中函数222,21xyxy的图象与函数2xy（中间虚线图

形）相比：①线型名称都叫线；②顶点相同吗？，坐标为（）；③对称轴相同吗？，对称轴为；④开口方向相同吗？它们的开口方向为；开口大小相同吗?，a越大，开口越。四．观察右图函数222,21xyxy的图象与函数2xy（中间图形），模仿上题的方法比较三

条抛物线的异同。相同点：。不同点：。五．归纳y=ax2（a≠0）的图象特征：x„-3-2-10123„y„„x„-3-2-10123„y„„xyyxOO(1)二次函数y=ax2的图象是一条线(2)抛物线y=ax2的对称轴是轴.顶点在原点；当a>0时，抛物线开口向，顶点是抛物形的最低点；当a<

0时，抛物线开口向，顶点是抛物线的最点.(3)|a|越大，抛物线y=ax2的开口越。六．新知体验【A层】1、若抛物线2axy开口向上，则a0；若抛物线2axy开口向下，则a0.2、若抛物线23xmy开口向下，则m

.3、函数22xy图象是线，开口向，顶点坐标为，对称轴是，顶点是抛物线的最（填“高”或“低”）点，在这点的函数值（就是y的值）最（填“大”或“小”），在对称轴左侧，y随x的增大而.4、函数221xy图象是线，开口向，顶点坐标为，对称轴是，顶点是抛物线的最（填“高”或“低”）

点，在这点的函数值（就是y的值）最（填“大”或“小”），当x>0时，y随x的增大而.【B层】5、在同一坐标系中：①y=212x，②y=-x2，③y=2x2这三个函数图象开口最大的是.6、抛物线25xy必经过点（0，）；若抛物线2axy经过点（1，2），则a=.7、若点（-1，-2）在抛

物线2axy上，则a=.【C层】8、如图，直线a的解析式是；直线b的解析式是；直线c的解析式是；直线d的解析式是；y轴的解析式是.9、一条隧道的截面如图，它的上部是半圆，半径为r，下部是矩形，矩形的一边AB长为3m，求隧

道的截面积S（m2）与上部半圆半径r(m)的函数关系式.10、已知抛物线的顶点在原点，对称轴是y轴，且经过(-3,2).求此抛物线的解析式，并指出x>0时，y随x的变化情况.dcba-3-2-1-4-3-2-1321

43210yxrDCBA【预学收获】通过以上的预学，思考如下几点：1.你知道二次函数2axy的图象特征吗？【预学中我的不明之处】导学案【学习目标】1.会用描点法作出函数y=ax2的图象，并根据图象认识和理解其性质；2．参

与探索二次函数y=ax2的图象和性质的过程，体会数形结合的思想和方法.3.核心价值点：培养学生的几何直观和数形结合思想，发展学生的应用意识。【分层达标】【A层】1.抛物线y=4x2的开口方向是，顶点坐标是，对称轴是.抛物线y=-14x2的开口方向是，顶点坐标是，对称轴是.2

.二次函数y=ax2与y=2x2，开口大小，形状一样，开口方向相反，则a=.3．在抛物线y=3x2中，当x>0时，y随x的增大而。在抛物线y=-x2中，当x>0时，y随x的增大而。4．在同一坐标系中：①y=212x，②y=-x2，③y=2x2这三个函数图象开口最

大的是，开口最小的是，开口向下的是。5.抛物线25xy的顶点坐标是且过A（—2，）6.抛物线2axy过A（—1，2），试判断B（—2，—3），是否在抛物线上。【B层】7.若二次函数22(1)mymx的图象开口向下,则m.8.把抛物线24yx绕其顶点旋转180,得到的抛物线解析式

为.【C层】9.已知直线ykx与抛物线2yax都经过点(-1,6).(1)求直线及抛物线的解析式；(2)判断点(,ka)是否在抛物线上；(3)若点(,ma)在抛物线上,求m的值.训练案【A层】1、二次函数221xy的

顶点坐标是，对称轴是直线。2、二次函数241xy的图象开口，当x＞0时，y随x的增大而；当x＜0时，y随x的增大而；当x＝0时，函数y有最值是。3、二次函数23xy的图象开口，当x＞0时，y随x的增大

而；当x＜0时，y随x的增大而；当x＝0时，函数y有最值是。4、已知点A（2，1y），B（4，2y）在二次函数23xy的图象上，则1y2y.5、已知点A（－2，1y），B（4，2y）在二次函数)0(

2aaxy的图象上，则1y2y.6、抛物线221xy不具有的性质是（）A．开口向下；B．对称轴是y轴；C．当x＞0时，y随x的增大而减小；D．函数有最小值7、抛物线2228,5,41xyxyxy共有的性质是（）A．开口方向相同B．开口大小相同C．当x＞0时，y随x的增大而增大D．对

称轴相同8、已知抛物线2axy经过点A（1，－4）.求:（1）x＝4时的函数值；（2）y＝－8时的x的值。【B层】9、已知抛物线mmxmy2)1(的开口向下，则m的值为。10、已知抛物线24xy与直线1kxy有唯一交点，求k的值。【C层】11、已知P（x，y）是抛物线

2xy第三象限内的一点，点A的坐标为（4，0），求OPA的面积S与x的函数关系式。