【文档说明】《二次函数y=ax2 bx c(a≠0)的图象与性质》PPT课件2-九年级下册数学北师大版.ppt，共(12)页，1.237 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-15320.html

以下为本文档部分文字说明：

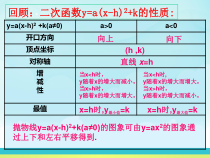
回顾：二次函数y=a(x-h)2+k的性质:y=a(x-h)2+k(a≠0)a>0a<0开口方向顶点坐标对称轴增减性最值向上向下(h,k)直线x=h当x<h时，y随着x的增大而减小。当x>h时，y随着x的增大而增大。当x<h时,y随着x的增大而增大。当x

>h时，y随着x的增大而减小。x=h时,y最小值=kx=h时,y最大值=k抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.二次函数y＝ax2＋bx＋c（a≠0）的图象和性质1、会将二次函数一般式:y＝ax2＋bx＋c（a≠0）化为y=

a(x-h)2+k（a≠0）的形式.2、熟记顶点坐标公式，会求对称轴及顶点坐标。3、掌握二次函数y=ax2+bx+c的图象和性质。学习目标如何将转化成的形式？探究二次函数的图象和性质216212xxy216212xxy216212xxy（x-h）+k2y=a（x-6）+3

2=21=（x2-12x）+2121=（x2-12x+36）-18+2121+36-36仔细阅读课本P37----P38“探究”上，思考：1.如何获得二次函数的图象2.y=-2x2-4x+1化成顶点式为：.y=-2(x+1)2+3自学

指导（1）216212xxy仔细阅读课本P38“探究”下----P39练习以上：1、理解记忆y=ax2+bx+c（a≠0）化成顶点式为：abacabxay44)2(22自学指导（2）对称轴是：顶点是：(,)ab2abac442ab2直线x=写出下列抛物线的开口方向、对称轴和顶

点：例xxy232解：313222ab313420344422abac开口方向：向上31x对称轴：直线），顶点坐标：（31-31-写出下列抛物线的开口方向、对称轴和顶点：检测：（一）xxy2)1(23421)2(2xxy检测：（

二）二次函数y=-2x2+6x-1当x时，y随x的增大而增大，当x时，y有最值，等于2323大271.抛物线y=x2-4x+3与y轴的交点坐标是，与x轴的交点坐标是。(0,3)(1,0)或（3，0）检测：（三）y=ax2+bx+c

(a≠0)a>0a<0开口方向顶点坐标对称轴增减性最值向上向下(,)当x<时，y随着x的增大而减小。当x>时，y随着x的增大而增大。当x<时,y随着x的增大而增大。当x>时，y随着x的增大而减小。x=时,y最小值=x=时,y最大值=小结：y=ax

2+bx+c的图象和性质ab2abac442ab2ab2ab2ab2ab2ab2abac442abac442ab2直线x=作业：必做题：1、求出下列抛物线的开口方向，对称轴和顶点坐标．①y=2x2

-4x+5②y=-x2+2x-32、二次函数y=-3x2+12x-1当x时，y随x的增大而增大，当x时，y随x的增大而减小．选做题：3.求出抛物线y=x2-3x-4与x轴的交点坐标，与y轴的交点坐标日清题：课本P41第6题（1）--（3）