【文档说明】《复习题》课后习题3-八年级下册数学北师大版.doc，共(3)页，95.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-15061.html

以下为本文档部分文字说明：

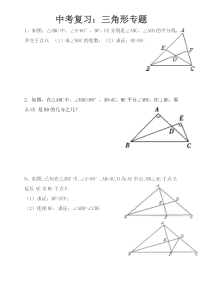
中考复习：三角形专题1、如图，△ABC中，∠A=60°，BF、CE分别是∠ABC、∠ACB的平分线，并交于点O．（1）求∠BOC的度数；（2）求证：OE=OF．2．如图，在△ABC中，∠BAC=90°，AB=AC，BE平分∠ABC，CE⊥BE，那么CE•是BD的几分之几？3、

如图,已知在△ABC中,∠A=90°,AB=AC,D为AC中点,DB⊥AE于点E,延长AE交BC于点F.（1）求证：BF=2CF；（2）连接DF，求证：∠ADB=∠CDF.1、如图，△ABC中，∠A=60°，BF、CE分别是∠ABC、∠ACB的平分线，并交于点O．（1）求∠BOC的度数

；（2）求证：OE=OF．证明：在CB上截取CG=CF，连接GO，由三角形内角和定理，在△ABC中，2∠FBC+2∠ECB+60°=180°，解得：∠FBC+∠ECB=60°，在△OBC中，∠BOC=180°-（∠FBC+∠ECB

）=180°-60°=120°，∴∠FOE=∠BOC=120°，在△CFO和△CGO中，CF＝CG,∠FCO＝∠GCO,CO＝CO∴△CFO≌△CGO（SAS），∴∠FOC=∠GOC，FO=GO，由∠BOG+∠GOC=120°，又∵

∠BOG+2∠GOC=180°，解得：∠BOG=∠GOC=∠FOC=60°在△BEO和△BGO中，∠EBO＝∠GBO,∠EOB＝∠GOB,BO＝BO∴△BEO≌△BGO（AAS），∴EO=OG，∴FO=EO．2．如图1-19，在△ABC中，∠BAC=90°，AB=AC，BE

平分∠ABC，CE⊥BE，那么CE•是BD的几分之几？解：延长BA与CE的延长线交于点F∵CE⊥BE,BE平分∠ABC∴△CBF是等腰三角形∴BE为CF边的中线∴CE=1/2CF∵∠ADB=∠CDE∴∠ABD=∠ACF（

等角的余角相等）∵AB=AC,∠BAD=∠CAF∴△BAD≌△CAF(ASA)∴BD=CF∴CE=1/2BD3、如图,已知在△ABC中,∠A=90°,AB=AC,D为AC中点,DB⊥AE于点E,延长AE交BC于点F.（1）求证：BF=2CF；（2）连接DF，求证：∠ADB=∠CD

F.12CDCFABBF12ADCFABBF（1）证明：过点D作DG∥AF交CF于点G∵D为AC中点∴CG=FG=CF易证△ADE∽△BAE∴∴BE=2AE=4DE又∵DG∥AF∴BF=4FG∴BF=2CF

（2）证明：过点D作DG∥AF交CF于点G∵,AD=CD∴,又∠ABF=∠C=45°∴△ABF∽△DCF∴∠CDF=∠BAF又∠BAF=∠ADB∴∠CDF=∠ADB12ADDEAEABAEBE12