【文档说明】《多边形的内角和》教学设计3-八年级下册数学北师大版.doc，共(3)页，60.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14969.html

以下为本文档部分文字说明：

课题多边形的内角和与外角和学习目标了解多边形的定义，以及多边形的顶点、边、内角、外角、对角等概念，掌握多边形的内角和定理。②通过动手实践,探究思索,交流互助。能将多边形问题转化为三角形问题。从而深刻理解多边形内角和公式的推导,并会加以运用。③认识特殊的的多边形——正多边形。教学重点掌握多边形

的内角和定理，会用多边形内角和定理解决简单问题。教学难点探索多边形的内角和定理的过程及其应用。教学方法学生先预习、自学，教师再适时点拨、归纳一、前置学习（一）【知识准备】1、三角形：由不在同一条直线上的三条线段所组成的图形。2、三角形的内角和定理3、多边形的

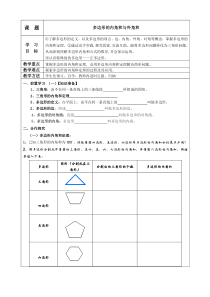
定义：在平面上，由不在同一条直线上的叫做多边形。2、多边形的边：组成叫做多边形的边。4、多边形的对角线：连接叫做多边形的对角线。5、多边形的内角：多边形叫多边形的内角。二、合作探究（一）多边形内角和定理：1、已知三角形的内角和为180。，你能猜想四边形、五边形、

六边形等多边形的内角和分别是多少吗？2、将多边形分割成不重叠的三角形，求四、五、六、七边形的内角和，并猜想n边形的内角和，将结果填入下表：多边形图形（分割成在三角形）分割出的三角形的个数多边形的内角和三角形四边形五边形六边形小结：多边形的内角和定理：。3、例题精讲：例1、一个多边形的内角和等

于1080度，这个多边形的边数是多少？4、想一想，议一议：①一个多边形的边都相等，它的内角一定都相等吗？②一个多边形的内角都相等，它的边一定都相等吗？③正三角形、正四边形、正五边形、正六边形、正八边形的内角分别是多少度？例2、正六边形的每个内角的度数是多少？试猜想正n边

形的每个内角的度数是多少。（三）巩固练习：1、一个五边形有三个内角是直角，另两个内角都等于n度，求n。2、过某个多边形一个顶点的对角线有10条，求这个多边形的内角和。3、若一个多边形，除了一个内角外，剩下的各内角之

和为2000度，求这个凸多边形的边数。四、当堂检测五、拓展延伸一个多边形截去一个角（不过顶点）后，形成的新的内角和是2520度，那么原多边形的边数是多少？六、课堂小结：1、通过学习，谈谈你的收获。2、说说你的困惑，让我们一起解决。当堂检测：1、9边形的内角和是，12边形

的内角和是2、已知多边形的内角和为1440°，则这个多边形的边数为3、正八边形的内角和是，它的每个内角的度数是4、一个多边形的边数增加1，则内角和增加的度数是。5、过某个多边形的一个顶点连接所有的对角线，将这个多边形分成5个三角形，这个多边形是边形，它的内角和是。6

、一个多边形从一个顶点可引对角线3条，则这个多边形的内角和等于（）度。A、360B、540C、720D、9007、一个凸多边形的一个内角的补角与其他内角的和恰好为660度，求这个凸多边形的边数。七边形n边形教学反思：以

四边形为研究对象，在知识和方法上有了突破之后，顺势提出五边形、六边形、七边形、八边形的内角和问题，这既是数学本身发展的需要，更是满足学生刚刚燃烧起来的探究欲望的需要，学生对教学的第三次突破也就自然不期而

至了．值得注意的是：如果说对四边形的研究带有很浓的“摸着石头过河”的感觉，那么这一环节的探究就显得很开放了，学生的自主地位很明显，而这正是数学发展的必然规律，学生认知发展的规律．可以看出：“让学生经历数学发展

的过程”这是教师努力追求的．本节课特别重视在解决问题和证明定理时展示数学思维过程，重视学生发现问题、提出问题的能力，使学生通过做数学、思数学、玩数学去感悟数学的严谨、力量、趣味和魅力．