【文档说明】《直角三角形斜边中线性质》PPT课件1-九年级上册数学华师大版.ppt，共(17)页，6.724 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14334.html

以下为本文档部分文字说明：

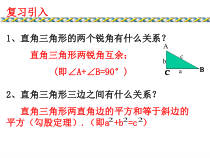
复习引入ACBCBC1、直角三角形的两个锐角有什么关系？直角三角形两锐角互余；(即∠A+∠B=90°)2、直角三角形三边之间有什么关系？直角三角形两直角边的平方和等于斜边的平方（勾股定理）.（即a+b

=c）222cba直角三角形的性质华师版九年级上册解直角三角形第2课时李淑平掌握直角三角形的性质，能利用直角三角形的性质进行有关的计算和证明.学习目标：掌握直角三角形的性质，能利用直角三角形的性质进行有关的计算和证明.掌握直角三角

形的性质，能利用直角三角形的性质进行有关的计算和证明.画Rt△ABC,并画出斜边AB上的中线CD，先观察，再量一量，看看CD与AB有什么关系.大家一定发现：CD恰好是AB的一半.动手操作，探索新知你能证明这一结论吗?三角形中，如果遇到中点问题你是如何考虑的？下面我们用演绎推理来证明这

一猜想已知：在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线.求证：CD=ABACBDE方法1：延长CD至点E，使DE=CD，连结AE、BE.211.中线倍长法方法2：过点A作AE∥BC交CD的延长线于点E，连结BE.方法3：取AC的中点E，连结DE.ACBD

E2.平行加中点造全等E3.有中点考虑中位线已知：在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线.求证：CD=AB21已知：在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线.求证：CD=AB21已知：在Rt△ABC中，∠ACB=90°，CD是斜边AB上

的中线.求证：CD=AB21由此，我们得到直角三角形的又一条性质：直角三角形斜边上的中线等于斜边的一半.几何语言可表示为：在△ABC中，∠ACB=90°，∵CD是斜边AB上的中线，∴CD=AB21运用新知2、在△ABC中，CD⊥AB于点D，E是AC的中点，若

AD=6，DE=5，则CD的长等于.3、在四边形ABCD中,∠ABC=∠ADC=90°，M、N分别是AC、BD的中点.求证：（1）MD=MB；（2）MN⊥BD81、直角三角形斜边上的中线把这个三角形分成两个三角形.等腰4、已知：在△ABC中，∠ACB=90°，∠A=

30°.求证：BC=AB214、已知：在△ABC中，∠ACB=90°，∠A=30°.求证：BC=AB21在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.由此可得性质3的推论：几何语言表示：在△ABC，∠ACB=90°,∠A=30°∴BC=AB21

1、在△ABC中，∠C=90°，AC=12，BC=5，则AB边上的中线的长为.2、在Rt△ABC中，CD是斜边AB上的中线，∠DCA=20°，则∠A=，∠B=.3、若一个等腰三角形的底角是15°，腰长为6cm，

则这个等腰三角形的面积为.当堂达标6.520°70°9cm24、在△ACD中，CE、DB分别是AD、AC边上的高，M、N分别CD、BE的中点.试判断MN与BE的关系，并说明理由.解：MN垂直平分BE.理由如下：连结BM、EM.∵CE、DB是AD、AC边

上的高，∴△ECD、△BCD是直角三角形.∵M是CD的中点，∴EM=CD，BM=CD，∴EM=BM.∵N是BE的中点，∴MN垂直平分BE.2121课堂小结：1、你学习了直角三角形的哪些性质？（1）直角三角形的两锐角互余；（2）直角三角形两直角边的平方和等于斜边

的平方；（3）直角三角形斜边上的中线等于斜边的一半；（4）直角三角形30°锐角所对的直角边等于斜边的一半.2、通过定理的学习过程给你带来了哪些收获？作业必做题：课本104页练习2题，105页习题3题选做题：走进

中考在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连结AM.（1）EF=AC；（2）若∠BAC=45,试判断线段AM,DM,BC之间的数量关系.21