【文档说明】《阅读材料 四边形的变身术》导学案-八年级下册数学华师大版.doc，共(4)页，237.500 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-14191.html

以下为本文档部分文字说明：

1平行四边形复习课导学案--------------《中点四边形》班别：姓名：学号：一、复习（1）什么是三角形的中位线？（2）三角形中位线的性质是什么？二、新课导学1、中点四边形的定义：依次连接任意一个四边形各边中点所得的四边形叫

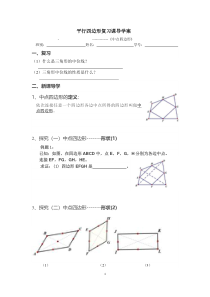
做中点四边形。2、探究（一）中点四边形-------形状(1)例题1：已知：如图，在四边形ABCD中，点E，F，G，H分别为各边中点。连接EF，FG，GH，HE。求证：(1)四边形EFGH是。3、探究（二）中点四边形--

-----形状(2)（1）（2）（3）2（4）（5）(6)（1）平行四边形的中点四边形是_________；（2）矩形的中点四边形是_______________；（3）菱形的中点四边形是______________

__；（4）正方形的中点四边形是______________；（5）等腰梯形的中点四边形是_____________；（6）直角梯形的中点四边形是_______决定中点四边形形状的主要因素是四边形ABCD的对角线的长度和位置。概括规律：（1）若对角

线的四边形，则中点四边形为（2）若对角线的四边形，则中点四边形为（3）若对角线的四边形，则中点四边形为3、探究（三）中点四边形的性质-----周长与面积例题：已知：如图，在四边形ABCD中，点E，F，G，H分别为各边中点

。连接EF，FG，GH，HE。已知AC=a,BC=b,四边形ABCD的面积为S.求证：(2)四边形EFGH的周长是(3)四边形EFGH的面积是规律总结：探究中点四边形周长与原四边形的关系（1）中点四边形的周长是。（2）中点四边形的面积是。3三、

学一致用，能力提升（中考连接1）练习（一）如图，四边形中ABCD中，AC=a，BD=b，且AC垂直于BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2，如此进行下去，得到四边形AnBnCnDn。下列结论：①四

边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是；④四边形AnBnCnDn的面积是。正确的有（）。A:①②B:②③C:②③④D:①②③④四、课后提高，挑战自我练习（二）如图所示，在Rt△ABC中，∠A=90°，DE∥BC，F，G，H，I分别是

DE，BE，BC，CD的中点，连接FG，GH，HI，IF，FH，GI．对于下列结论：①∠GFI=90°；②GH=GI；③GI=（BC﹣DE）；④四边形FGHI是正方形．其中正确的是（请写出所有正确结论的序号）4（中考连接2）练习（三）如图1,在正方形

ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AFDE(不须证明).如图①,若点E、F不是正方形ABCD的边BC、CD的中点,但满足,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)(2

)如图②,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)如图③,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点

,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程图①图②图③