【文档说明】2021年人教版高中数学必修第二册(精练)第九章《知识总结及测试》（解析版）.doc，共(18)页，1.046 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-39344.html

以下为本文档部分文字说明：

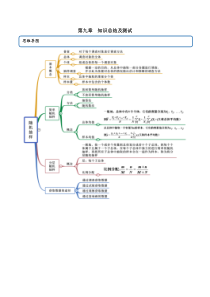
第九章知识总结及测试思维导图单元测试一、单选题（每题只有一个选项为正确答案，每题5分，8题共40分）1．（2021·浙江高一单元测试）3个数1，3，5的方差是（）A．23B．34C．2D．83【答案】D【解析】

由题得3个数的平均数为3，所以22221813335333S．故选：D2．（2020·全国高一课时练习）从某班50名同学中选出5人参加户外活动，利用随机数表法抽取样本时，先将50名同学按01，02，„„，50进行编号，然后从随机数表的第1行第5列和第6列

数字开始从左往右依次选取两个数字，则选出的第5个个体的编号为（）（注：表为随机数表的第1行与第2行）A．24B．36C．46D．47【答案】A【解析】由随机数表．抽样编号依次为43，36，47，36前面出现过去掉，46，24，第5个是24．故选：A．3．（2020·黑龙江齐齐哈尔市实

验中学高二期中（文））为了解一片大约一万株树木的生长情况，随机测量了其中100株树木的底部周长（单位：㎝）.根据所得数据画出的样本频率分布直方图如图，那么在这片树木中，底部周长小于110㎝的株树大约是（）A．3000B．6000C．7000D．8000【答案】C【

解析】由频率分布直方图可得，样本中底部周长小于110㎝的概率为(0.0010.0020.004)100.7，因此在这片树木中，底部周长小于110㎝的株树大约是100000.77000.故选：C.

4．（2021·浙江高一单元测试）某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番.为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例.得到如下扇形统计图：则下面结论中不正确．．．的是（）A．新农村

建设后，种植收入略有增加B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入不变D．新农村建设后，种植收入在经济收入中所占比重大幅下降【答案】C【解析】因为该地区经过一年的新农村建设，农村的经济收入增加了一倍，不妨设建设前的经济收入为m，则建设后的经济收入为2m，A选项，

从扇形统计图中可以看到，新农村建设后，种植收入比建设前增加237%60%14%mmm，故A正确；B选项，新农村建设后，其他收入比建设前增加25%4%6%4%mmmm，即增加了一倍以上，故B正确；C选项，

养殖收入的比重在新农村建设前与建设后相同，但建设后总收入为之前的2倍，所以建设后的养殖收入也是建设前的2倍，故C错误；D选项，新农村建设后，种植收入在经济收入中所占比重由建设前的60%降为37%，故D正确；故选：C.5．（2021·

全国高一课时练习）如图，是根据某班学生在一次数学考试中的成绩画出的频率分布直方图，若由直方图得到的众数，中位数和平均数（同一组中的数据用该组区间的中点值为代表）分别为,,abc，则（）A．bacB．abcC．2acb

D．2bca【答案】B【解析】由频率分布直方图可知：众数7080752a；中位数应落在70-80区间内，则有：0.01100.015100.015100.03(70)0.5b，解得：22017333b

；平均数4050506060700.01100.015100.01510222c70808090901000.03100.025100.00510222=4.5+8.25+9.75+22.5+21.25+4.75=71所以abc故选：B6．（20

21·全国高一课时练习）在发生某公共卫生事件期间，我国有关机构规定：该事件在一段时间没有发生规模群体感染的标志为“连续10天每天新增加疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（）A．甲地总体均值为3，中位数为4B．乙地总体均值为2，总体方差大于0C

．丙地中位数为3，众数为3D．丁地总体均值为2，总体方差为3【答案】D【解析】对于A选项，反例：0、0、1、1、4、4、4、4、4、8，满足中位数为4，均值为3，与题意矛盾，A选项不合乎题意；对于B选项，反例：0、1、1、1、1、1、1、2、4、8，满足均值为2，方差大于0

，与题意矛盾，B选项不合乎题意；对于C选项，反例：0、1、1、3、3、3、3、3、3、8，满足中位数为3，众数为3，与题意矛盾，C选项不合乎要求；对于D选项，将10个数由小到大依次记为1x、2x、3x、4x、5x、6x、7x

、8x、9x、10x，假设108x，若均值为2，则方差为10221021223.61010iixxs，矛盾，故108x，假设不成立，故丙地没有发生规模群体感染，D选项合乎要求.

故选：D.7．（2020·全国高一课时练习）在一次数学测试中，高二某班40名学生成绩的平均分为82，方差为10.2，则下列四个数中不可能是该班数学成绩的是（）A．100B．85C．65D．55【答案】D【解析】方差22110.2ni

ixxsn，40n402110.240408iixx若存在55x，则402221()(8255)729408iixxxx导致方差必然大于10.2，不符合题意.55不可能是该班数学成绩故选：D.8．（2021·全国高一课时练

习）某校高一年级随机抽取15名男生，测得他们的身高数据，如下表所示：编号身高编号身高编号身高117361691116821797177121753175817513172417391741416951701018215176那么这组数据的第80百

分位数是（）A．175B．176C．176.5D．170【答案】C【解析】这15个数据按照从小到大排列，可得168,169,169，170,172,173,173,174,175，175,175,176,177,179,1

82，80%1512，第80百分位数为第12项与第13项数据的平均数，即1176177176.52.故选：C二、多选题（每题不止有一个选项为正确答案，少选且正确得2分，每题5分，4题共20分）9．（2020·全国）某健身房为了

解运动健身减肥的效果，调查了20名肥胖者健身前（如直方图（1）所示）后（如直方图（2）所示）的体重（单位：kg）变化情况：对比数据，关于这20名肥胖者，下面结论正确的是（）A．他们健身后，体重在区间90,100内的人

数较健身前增加了2人B．他们健身后，体重原在区间100,110内的人员一定无变化C．他们健身后，20人的平均体重大约减少了8kgD．他们健身后，原来体重在区间110,120内的肥胖者体重都有减少【答案】AD【解析】体重在区间

90,100内的肥胖者由健身前的6人增加到健身后的8人，增加了2人，故A正确；他们健身后，体重在区间100,110内的百分比没有变，但人员组成可能改变，故B错误；他们健身后，20人的平均体重大约减少了0.3950.51050.21150.1850.4950.5

1055kg，故C错误；因为图（2）中没有体重在区间110,120内的人员，所以原来体重在区间110,120内的肥胖者体重都有减少，故D正确.故选：AD.10．（2021·全国高一课时练习）下列命题中是真命题的有（）A．有A，B，C三种个体按312︰︰的比例分层

抽样调查，如果抽取的A个体数为9，则样本容量为30B．一组数据1，2，3，3，4，5的平均数、众数、中位数相同C．若甲组数据的方差为5，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是甲D．某一

组样本数据为125，120，122，105，130，114，116，95，120，134，则样本数据落在区间114.5124.5，内的频率为0.4【答案】BD【解析】对于选项A：根据样本的抽样比等于各层的抽样比，样本容量为3918123，故选项A不正确；对于选项B：数据1，

2，3，3，4，5的平均数为11234535，众数和中位数都是3，故选项B正确；对于选项C：乙组数据的平均数为156910575，乙组数据的方差为222221576797107574.45

5，所以这两组数据中较稳定的是乙，故选项C不正确；对于选项D：样本数据落在区间114.5124.5，有120，122，116，120有4个，所以样本数据落在区间114.5124

.5，内的频率为.40410，故选项D，故选：BD11．（2021·全国高一课时练习）下列命题是真命题的有（）A．有甲、乙、丙三种个体按3:1:2的比例分层抽样调查，如果抽取的甲个体数为9，则样本容量为30B．数据1，2，3，3，4，5的平均数、众数、中位数相同C．

若甲组数据的方差为5，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是乙D．一组数6，5，4，3，3，3，2，2，2，1的85%分位数为5【答案】BCD【解析】对于A项，乙、丙抽取的个体数分别为36,，则样本容量为36918

，故A错误；对于B项，平均数为12334536，中位数为3，众数为3，故B正确；对于C项，乙的平均数为56910575，方差为22222212221232555s，则这两组数据中较稳定的是乙，故C正确；对于D项，将该组数据总小到大排列1,2,2,2,3

,3,3,4,5,6，由1085%8.5，则该组数据的85%分位数为5，故D正确；故选：BCD12．（2021·全国高一课时练习）统计某校1000名学生的某次数学同步练习成绩(满分150分)，根据成绩依次分

为六组，90,100，100,110，110,120，130140,，140,150，得到如图所示的频率分布直方图，则下列说法正确的是（）A．0.031mB．0.31mC．100分以下的人数为60D．成绩在区间120.140

的人数有470人【答案】ACD【解析】对选项A，B，由图可知，100.0200.0160.0160.0110.0061m，解得0.031m，故A说法正确，B错误；对选项C，因为100分以下的频率为0.00610=0.06，所以100分以下的人数

为10000.06=60，故C说法正确；对选项D，成绩在区间120,140内的频率为0.03110+0.016100.47，所以成绩在区间120.140的人数有10000.47470人，故D说法正确.故选：ACD三、填空题（每题5分，4题共20分）13．（2021

·全国高一课时练习）A工厂年前加紧手套生产，设该工厂连续5天生产的手套数依次为x1，x2，x3，x4，x5(单位：万只)，若这组数据x1，x2，x3，x4，x5的方差为1.44，且x12，x22，x32，x42，x52的平均数为4，则该工厂这5天平均每天生产手套___________万只.【答案】

1.6【解析】设每天生产平均值为x依题意得222221234551.447.2xxxxxxxxxx所以2222221234512345257.2xxxxxxx

xxxxx又因为22222123455420xxxxx，123455xxxxxx所以22057.2x解得1.6x故答案为：1.614．（2021·全国高一课时练习）已知一

组数据3,2,4,5,1,9aa的平均数为3（其中aR），则中位数为_____________．【答案】3.5【解析】解：因为数据3,2,4,5,1,9aa的平均数为3，所以32451936aa，解得2a，所以则组数据分别是3,4,4,3,1,9，按从小到大

排列分别为3,1,3,4,4,9，故中位数为343.52故答案为：3.515．（2021·浙江高一单元测试）为了了解初中生的身体素质，某地区随机抽取了n名学生进行跳绳测试，根据所得数据画样本的频率分布直方图如图所示，且从左到右第一小组的频数是100

，则n_____.【答案】1000【解析】由频率分布直方图知，从左到右第一小组的频率为0.004250.1，且从左到右第一小组的频数是100，所以100=10000.1n.故答案为：100016．（2021·浙江高一单元测试

）某市A、B、C三个区共有高中学生20000人，其中A区高中学生7000人，现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600人的样本进行学习兴趣调查，则A区应抽取__________________.【答案】210【解析】由题意知A区在样本中的

比例为700020000∴A区应抽取的人数是700060021020000.故答案为：210．四、解答题（17题10分，其余每题12分，6题共70分）17．（2020·全国高一课时练习）为了落实习主席提出“绿水青山就是金山银山”的环境治理

要求，某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x(吨)，一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年200位居民每人的月均用水量(单位：吨)，将数据按照[

0，1)，[1，2)，„，[8，9)分成9组，制成了如图所示的频率分布直方图,其中0.4ab.（1）求直方图中,ab的值，并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表)；（2）设该市有40万居民，估计全市居民中月均用水量不低于2吨

的人数，并说明理由；（3）若该市政府希望使85%的居民每月的用水量不超过标准x(吨)，估计x的值，并说明理由.【答案】（1）0.15a，0.06b；4.07（2）35.2万；（3）5.8x【解析】（1）由频率分布直方图可得0.04+0.08+

0.200.260.040.021aab，又0.4ab，则0.15a，0.06b，该市居民用水的平均数估计为：0.50.041.50.082.50.153.50.204.50.26x5.50.156.50.

067.50.048.50.024.07；（2）由频率分布直方图可得，月均用水量不超过2吨的频率为：0.040.080.12，则月均用水量不低于2吨的频率为：10.120.88，所以全市40万居民中月均用水量不低于2吨的人数为：400.88

35.2（万）；（3）由频率分布直方图知月均用水量不超过6吨的频率为：0.88，月均用水量不超过5吨的频率为0.73，则85%的居民每月的用水量不超过的标准x（吨），56x，0.730.15(5)0.85x，解得5.8x，即标准为5.8吨.18．（2020·全国高一课时练习

）成都七中为了解班级卫生教育系列活动的成效，对全校40个班级进行了一次突击班级卫生量化打分检查（满分100分，最低分20分）.根据检查结果：得分在[80,100]评定为“优”，奖励3面小红旗；得分在[60,80)评定为“良

”，奖励2面小红旗；得分在[40,60)评定为“中”，奖励1面小红旗；得分在[20,40)评定为“差”，不奖励小红旗.已知统计结果的部分频率分布直方图如图：（1）依据统计结果的部分频率分布直方图，求班级卫生量化打分检查得分的中位数；（2）学校用分层抽样的方法，从评

定等级为“良”、“中”的班级中抽取6个班级，再从这6个班级中随机抽取2个班级进行抽样复核，求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.【答案】（1）70分；（2）1415.【解析】（1）得分[20,40)的频率为0.005200.1；得分[

40,60)的频率为0.010200.2；得分[80,100]的频率为0.015200.3；所以得分[60,80)的频率为1(0.10.20.3)0.4设班级得分的中位数为x分，于是600.10.20.40.520x，解得70x所以班级卫生量化打分检

查得分的中位数为70分.（2）由（1）知题意“良”、“中”的频率分别为0.4,0.2又班级总数为40于是“良”、“中”的班级个数分别为16,8.分层抽样的方法抽取的“良”、“中”的班级个数分别为4,2因为评定为“良”，奖励2面小红旗，评定为“中”，奖励1面小红旗.所以抽取的2个班级获得的奖励小

红旗面数和不少于3为两个评定为“良”的班级或一个评定为“良”与一个评定为“中”的班级.记这个事件为A则A为两个评定为“中”的班级.把4个评定为“良”的班级标记为1,2,3,4.2个评定为“中”的班级标记为

5,6从这6个班级中随机抽取2个班级用点(,)ij表示，其中16ij.这些点恰好为66方格格点上半部分（不含ij对角线上的点），于是有366152种.事件A仅有(5,6)一个基本事件.所以114()1()11515PAPA所抽取的2个班级获得的奖励小红旗

面数和不少于3的概率为1415.19．（2020·全国高一课时练习）近年来，我国电子商务行业迎来了蓬勃发展的新机遇，但是电子商务行业由于缺乏监管，服务质量有待提高．某部门为了对本地的电商行业进行有效监管，调查了甲、乙两家电商的某种同类产品连续十天的销售额（单位：万元），得到如下茎叶图：（1）根据茎

叶图判断甲、乙两家电商对这种产品的销售谁更稳定些？（2）如果日销售额超过平均销售额，相应的电商即被评为优，根据统计数据估计两家电商一个月（按30天计算）被评为优的天数各是多少．【答案】（1）甲更稳定（2）甲15天，乙12天【解析】（

1）105107113115119126128132134141=12210x甲(万元)，22222221(105122)(107122)(113122)(115-122)(119122)(126122)10s

甲22(128122)(132122)22(134122)(141122)131，10711511711812312513213613914812610x乙(万元)22222221(107126)(115126)(

117126)(118126)(123126)(125126)10s乙222(136126)(139126)(148126)142.6因为22ss甲乙，所以甲电商对这种产品的销售更稳定.（2）由题中茎叶图可知，甲电商该类产品这10天的日销售

额数据超过122万元的为126，128，132，134，141，共5天，即评为优的频率为50.510，由此可估计一个月30天甲被评为优的天数为0.53015天，乙电商该类产品这10天的日销售额数据超过126万元的为132，136，139，148，共4天，即评为优的频率为.40410

，由此可估计一个月30天乙被评为优的天数为0.43012天.20．（2020·全国高一课时练习）2019年下半年以来，各地区陆续出台了“垃圾分类”的相关管理条例，实行“垃圾分类”能最大限度地减少垃圾处置量，实现垃圾资源利用，改善垃圾

资源环境，某部门在某小区年龄处于20,45岁的人中随机地抽取x人，进行了“垃圾分类”相关知识掌握和实施情况的调查，并把达到“垃圾分类”标准的人称为“环保族”，得到如图示各年龄段人数的频率分布直方图和表中的统计数据.组数分组“环保族”人

数占本组的频率第一组20,25450.75第二组25,3025y第三组30,35200.5第四组35,40z0.2第五组40,4530.1（1）求x、y、z的值；（2）根据频率分布直方图，估

计这x人年龄的平均值（同一组数据用该区间的中点值代替，结果按四舍五入保留整数）；（3）从年龄段在25,35的“环保族”中采取分层抽样的方法抽取9人进行专访，并在这9人中选取2人作为记录员，求选取的2名记

录员中至少有一人年龄在30,35中的概率.【答案】（1）2000.6256xyz；（2）30.75；（3）1318.【解析】（1）由题意得：450.752000.065250.6252000.0452000.0350.26xyz

；（2）根据频率分布直方图，估计这x人年龄的平均值为：22.50.327.50.232.50.237.50.1542.50.1530.75x；（3）从年龄段在25,35的“环保族”中采取分层抽样的方法抽取9人进行专访

，从25,30中选：25952520人，分别记为A、B、C、D、E，从30,35中选：20942520人，分别记为a、b、c、d，在这9人中选取2人作为记录员，所有的基本事件有：,AB、,AC、,AD、,AE、,Aa、

,Ab、,Ac、,Ad、,BC、,BD、,BE、,Ba、,Bb、,Bc、,Bd、,CD、,CE、,Ca、,Cb、,Cc、,Cd、,DE、,Da、,Db、,Dc、,Dd、,Ea、,Eb、,Ec、,Ed

、,ab、,ac、,ad、,bc、,bd、,cd，共36种，选取的2名记录员中至少有一人年龄在30,35包含的基本事件有：,Aa、,Ab、,Ac、,Ad、,Ba、,Bb、,Bc、,Bd、,Ca、,C

b、,Cc、,Cd、,Da、,Db、,Dc、,Dd、,Ea、,Eb、,Ec、,Ed、,ab、,ac、,ad、,bc、,bd、,cd，共26种，因此，选

取的2名记录员中至少有一人年龄在30,35中的概率26133618P.21．（2020·全国高一课时练习）A､B两同学参加数学竞赛培训，在培训期间，他们参加了8次测验，成绩(单位：分)记录如下：B同学的成绩不慎被墨迹污染(，分别用m，n表示).（1）

用茎叶图表示这两组数据，现从A､B两同学中选派一人去参加数学竞赛，你认为选派谁更好？请说明理由(不用计算)；（2）若B同学的平均分为78，方差s2=19，求m，n.【答案】（1）茎叶图答案见解析，选派B同学参加数学竞赛更好，理由见解析；（2）m=8，n=0.【解析】（1）A，B两同学参加了8次测

验，成绩(单位：分)茎叶图如下：由茎叶图可知，B同学的平均成绩高于A同学的平均成绩，所以选派B同学参加数学竞赛更好；（2）因为1(7384757370807685)788xmn，所以8mn①，因为222222221563(8)(2)27198Smn

，所以22(8)(2)4mn②，联立①②解得，8,0mn.22．（2021·浙江高一单元测试）微信是现代生活进行信息交流的重要工具，随机对使用微信的60人进行了统计，得到如下数据统计表

，每天使用微信时间在两小时以上的人被定义为“微信达人”，不超过两小时的人被定义为“非微信达人”．已知“非微信达人”与“微信达人”人数比恰为3∶2.使用微信时间(单位：小时)频数频率[0，0.5)30.05[0.5，1)xp[1，1.5)90.15[1.5，2)150.25[

2，2.5)180.30[2.5，3]yq合计601.00确定x，y，p，q的值，并补全频率分布直方图．【答案】9,6,0.15,0.10xypq，补全的频率分布直方图如图所示【解析】因为“非微信达人”与“微信达人”人数比恰为3∶2，所以39153182xy

，又因为39151860xy，所以解得9,6xy，所以960.15,0.106060pq，补全的频率分布直方图如图所示