【文档说明】2021年人教版高中数学必修第二册(精练)第七章《知识总结及测试》（解析版）.doc，共(12)页，1.168 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-39340.html

以下为本文档部分文字说明：

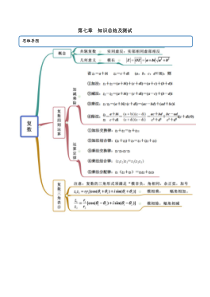
第七章知识总结及测试思维导图一、单选题（每题只有一个选项为正确答案，每题5分，8题共40分）1．（2020·全国高一课时练习）已知复数z对应的向量为OZ（O为坐标原点），OZ与实轴正方向的夹角单元测试为120

，且复数z的模为2，则复数z为（）A．13iB．13iC．13iD．13i【答案】D【解析】设复数在复平面内对应的点的坐标为,Zab，根据题意可画图形如图所示，2z，且OZ与x轴正方向的夹角为120，1a，3b，即点Z的坐标为13,或

1,3.13zi或13zi.故选：D2．（2020·全国高一课时练习）已知i是虚数单位，复数13i的虚部是（）A．1B．3C．13D．13i【答案】C【解析】由复数的概念知，复数13i的虚部是13，故选：C.3．（

2020·全国高一课时练习）.已知5,1,3,2OAOB，AB对应的复数为z，则z（）A．5iB．32iC．23iD．23i【答案】D【解析】由题可知2,3AB，故AB对应的复数为23zi，则23zi，故选：D.4．（2020·全国高一

课时练习）已知a为实数，若复数2(1)(1)zaai为纯虚数，则复数z的虚部为（）A．1B．2iC．D．2【答案】D【解析】由已知21010aa，解得1a，故2zi，其虚部为2，故选

：D.5．（2020·全国高一课时练习）设i是虚数单位，则2320192342020iiii的值为（）A．10101010iB．10111010iC．10111012iD．10111010i【答案

】B【解析】设2320192342020Siiii,可得：24201920320023420192020iSiiiii，则24201923020(1)22020iSiiiiii，20192420192020

23020(1)(1)202020201iiiSiiiiiiiiii，可得：2(1)(1)(1)20202020202112iiiiiSiiii，可得：20

21(2021)(1)1011101012iiiSii，故选：B.6．（2020·全国专题））若z=1+i，则|z2–2z|=（）A．0B．1C．2D．2【答案】D【解析】由题意可得：2212zii，则222212zzi

i.故2222zz.故选：D.7．（2020·全国高一课时练习）复数3aizai(其中aR，i为虚数单位)，若复数z的共轭复数的虚部为12，则复数z在复平面内对应的点位于()A．第一象限B．第二象限C．第三

象限D．第四象限【答案】A【解析】由题意得331313331010aiiaiaiazaaiii，∴31311010aiaz，又复数z的共轭复数的虚部为12，∴31102a，解得2a.∴5122zi

，∴复数z在复平面内对应的点位于第一象限.故选A.8．（2020·全国高一课时练习）计算1+i+i2+i3+…+i89的值为（）A．1B．iC．﹣iD．1+i【答案】D【解析】由等比数列的求和公式可得：1+i+i2+i3+…+i8990111ii

，而i90＝i88•i2＝i2＝﹣1，故1+i+i2+i3+…+i8990112121111iiiiii1+i，故选：D.二、多选题（每题不止一个选项为正确答案，每题5分，共

4题20分）9．（2020·全国高一课时练习）若复数z满足(1i)3iz（其中i是虚数单位），复数z的共轭复数为z，则（）A．|z|5B．z的实部是2C．z的虚部是1D．复数z在复平面内对应的点在第一象限【答案】ABD【解析】(1i)3iz，

3134221112iiiiziiii，2215z，故选项A正确，z的实部是2，故选项B正确，z的虚部是1，故选项C错误，复数2zi在复平面内对应的点为2,1，在第一象限，故选项

D正确.故选：ABD.10．（2020·全国高三专题练习）设i为虚数单位，复数()(12)zaii，则下列命题正确的是（）A．若z为纯虚数，则实数a的值为2B．若z在复平面内对应的点在第三象限，则实数a的取值范围是(,)122C．实数12a是zz

（z为z的共轭复数）的充要条件D．若||5()zzxixR，则实数a的值为2【答案】ACD【解析】()(12)2(12)zaiiaai∴选项A：z为纯虚数，有20120aa可得2a，故正确选项B：z在复平面内对应的点在第三象限，

有20120aa解得12a，故错误选项C：12a时，52zz；zz时，120a即12a，它们互为充要条件，故正确选项D：||5()zzxixR时，有125a，即2a，故正确故选：AC

D11．（2020·山东枣庄市·滕州市第一中学新校高二开学考试）下面关于复数的四个命题中，结论正确的是（）A．若复数zR，则zRB．若复数z满足2zR，则zRC．若复数z满足1Rz，则zRD．若复数1z，2z满足12zzR，则12

zz【答案】AC【解析】A选项，设复数(,)zabiabR，则(i,)zababR，因为zR，所以0b，因此zaR，即A正确；B选项，设复数(,)zabiabR，则22222zabiababi，因为2zR，所0a

b，若0,0ab，则zR；故B错；C选项，设复数(,)zabiabR，则22222211abiabizabiababab，因为1Rz，所以220bab，即0b，所以zaR；故C正确；D选项，设复数1(,)zabiabR

，2(,)zcdicdR，则12zzabicdiacbdadbci，因为12zzR，所以0adbc，若11ab，22cd能满足0adbc，但12zz，故D错误.故选：AC.12．（2020·全国高一课时练习）下列

关于复数的说法，其中正确的是（）A．复数,zabiabR是实数的充要条件是0bB．复数,zabiabR是纯虚数的充要条件是0b≠C．若1z，2z互为共轭复数，则12zz是实数D．若1z，2z互为共轭复数，则在复平面内它们所对应的点关于y轴对称【答案】AC【解析】对于A：

复数,zabiabR是实数的充要条件是0b，显然成立，故A正确；对于B：若复数,zabiabR是纯虚数则0a且0b≠，故B错误；对于C：若1z，2z互为共轭复数，设1,zabiab

R，则2,zabiabR，所以2122222zabiabiabbzia是实数，故C正确；对于D：若1z，2z互为共轭复数，设1,zabiabR，则2,zabiabR，所对应的坐标分别为,ab，,ab，这两点关于x轴对称，故D错

误；故选：AC三、填空题（每题5分，4题共20分）13．（2020·全国高一课时练习）已知复数12zi，那么1z_____________.【答案】1255i【解析】12zi，12zi，故1112121212121255

5iiiiiiz.故答案为：1255i.14．（2020·上海浦东新区）已知x、Ry，i为虚数单位，且2i1ixy，则xy____________．【答案】2【解析】21

2i1i1xxyy121xxyy故答案为：215．（2020·全国高一课时练习）已知i为虚数单位，复数z满足11izi，则z的共轭复数z为_____________.【

答案】i【解析】由11izi，得211111iiziiii，则zi.故答案为：i.16．（2020·全国高一课时练习）如果向量OZ对应复数4i，OZ绕点O按逆时

针方向旋转45后再把模变为原来的2倍得到向量1OZ，那么与1OZ对应的复数是_____________（用代数形式表示）.【答案】44i【解析】44cos90sin90ii.所求复数为4cos90sin902cos45sin45i2

242cos135sin135424422iii.故答案为：44i.四、解答题（第17题10分，其余每题12分，共70分）17．（2020·全国高一课时练习）已知复数22lg2132zmmmmi

（i为虚数单位），试求实数m分别取什么值时，z分别为：（1）实数；（2）虚数；（3）纯虚数.【答案】（1）2m；（2）,22,11,m；（3）0m.【解析】（1）由22210320mmmm，得2m，当2m时，z是

实数；（2）由22210320mmmm，得1m且2m，当,22,11,m时，z是虚数；（3）由题意得22320lg210mmmm，.即22320211mmmm，解得0m.当0

m时，z是纯虚数.18．（2020·全国高一课时练习）实数m取什么值时,复数22(56)(215)zmmmmi(1)与复数212i相等(2)与复数1216i互为共轭复数(3)对应的点在x轴上方.【答案】（1）m＝－1（2）m

＝1（3）m<－3或m>5.【解析】(1)根据复数相等的充要条件得22562{21512mmmm解得m＝－1.(2)根据共轭复数的定义得225612{21516mmmm解得m＝1.(3)

根据复数z的对应点在x轴的上方可得m2－2m－15>0，解得m<－3或m>5.19．（2020·全国高一课时练习）已知i是虚数单位，O为坐标原点，向量OA对应的复数为32i，将向量OA向上平移3个单位长度，再向左平移

2个单位长度，将得到的向量记为OA，分别写出：（1）向量OA对应的复数；（2）点O对应的复数；（3）向量AO对应的复数.【答案】（1）32i；（2）23i；（3）32i.【解析】如图所示，O为原点，点A的

坐标为3,2，向上平移3个单位长度，再向左平移2个单位长度后，点O的坐标为2,3，点A的坐标为1,5，坐标平移不改变OA的方向和模，（1）向量OA对应的复数为32i；（2）点O对应

的复数为23i；（3）向量AO对应的复数为32i.20．（2020·全国高一课时练习）已知复数211zii（i为虚数单位）.（1）求1z及1z；（2）当复数z满足34i1z时，求1zz的最大值与最小值.【

答案】（1）12z，12z；（2）最大值为171，最小值为171.【解析】复数221112122ziiiii.（1）12z，12z.（2）设复数,zxyixyR，341zi，22341xy，它表示复数z对应的

点到3,4的距离为1，构成的图形是圆心为3,4P，半径为1的圆，画出图形，如图所示，1z所对应的点为2,0A，则圆心P到点A的距离为2232417PA.因为1zz表示圆P上的点到点A的距离，所以1zz的最大值为117

1PA，最小值为1171PA.21．（2020·全国高一课时练习）已知复数1sin2izx，2(3cos2)izmmx（,,mxR），且12zz.（1）若0且0πx

，求x的值；（2）设()fx；①求()fx的最小正周期和单调递减区间；②已知当x时，12，试求cos(4)3的值.【答案】（1）6，23；（2）①周期T，单调减区间511[,]1212kk，kZ；②78【解析】由于12zz，

所以sin23cos2xmmx，故sin23cos2xx.（1）当0时，sin23cos20xx，则tan23x，由于0πx所以022πx，所以π23x或4π23x，所以π6x或2π3x.（2）由于sin23cos2xx，故

πsin23cos22sin23fxxxx.①函数fx的最小正周期为2ππ2T.由ππ3π2π22π232kxk，解得5π11πππ1212kxk，所以函数fx的单调递减区间为511[,]12

12kk，kZ.②依题意π1sin23cos22sin232x，所以π1sin234.所以ππcos4cos223622ππ2cos212sin2163

1721168.22．（2020·全国高一课时练习）在复平面内，平行四边形OABC的顶点O，A，C，对应复数分别为0，2i，13i．（1）求OB，CA及||OB，||CA；（2）设OCB，求cos．【答案】（1）14OBi，

||17OB；32CAi，||13CA；（2）210.【解析】（1）因为OBOAOC所以OB所对应的复数12(13)1(4)ziii所以(1,4)OB，22||1417OB因为CAOAOC所以CA所对应的复数22(13)32()z

iii所以(3,2)CA，22||3(2)13CA（2）由题,CBCO因为(2,1)CBOA，(1,3)COOC所以211(3)1CBCO，22||215CB，22||1(3)10CO所以2coscos,10

||||CBCOCBCOCBCO