【文档说明】2021年人教版高中数学必修第二册(精练)8.5《空间直线、平面的平行》（精炼）（解析版）.doc，共(26)页，1.569 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-39315.html

以下为本文档部分文字说明：

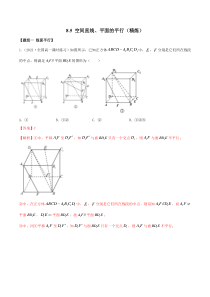
8.5空间直线、平面的平行（精炼）【题组一线面平行】1．（2021·全国高一课时练习）如图所示，已知正方体1111ABCDABCD中，E，F分别是它们所在线段的中点，则满足1//AF平面1BDE的图形为（）A．①B．①②C．②D．①②

③【答案】C【解析】①中，平移1AF至1DF，知1DF与面1BDE只有一个交点1D，则1AF与面1BDE不平行；②中，在正方体1111ABCDABCD中，E，F分别是它们所在线段的中点，则易知11//AFDE，而1AF平面1BDE，1DE平面1BDE，

故1//AF平面1BDE；③中，同①平移1AF至1DF，知1DF与面1BDE只有一个交点1D，则1AF与面1BDE不平行；故选：C．2．（2021·全国高一课时练习）已知正方体1111ABCDABCD中，E，F分别是它们所在线段的中点，则满足1//AF

平面1BDE的图形个数为（）A．0B．1C．2D．3【答案】B【解析】②中，11//AFDE，而1AF平面1BDE，1DE平面1BDE，故1//AF平面1BDE；①中，平移1AF至1DF，知1DF与面1BDE只有一个交点1D，则1AF与面1BDE不平行；③中，同样平移1AF至1DF

，知1DF与面1BDE只有一个交点1D，则1AF与面1BDE不平行；故选：B．3．（2020·济南大学城实验高级中学高一期中）如图，在正方体ABCD-A1B1C1D1中，已知E，F，G分别是线段A1C1上的点，且A1E＝EF＝FG＝GC1.则下列直线与平面A1BD

平行的是（）A．CEB．CFC．CGD．CC1【答案】B【解析】如图，连接AC，使AC交BD于点O，连接A1O，CF，在正方体ABCD­-A1B1C1D1中，由于111//,2AFACAFAC，又OC＝12AC，可得：11//,AFOCAFOC，即四边形A1OCF为平行四边形，可

得：A1O∥CF，又A1O⊂平面A1BD，CF⊄平面A1BD，可得CF∥平面A1BD，故选：B.4．（2021·全国高一）下列四个正方体图形中，AB、为正方体的两个顶点，MNP、、分别为其所在棱的中点，能得出//AB平面MNP的图形的序号是（）A．①③B．①④C．①③④D．②④【答案】B【解析】对

于①，如图，依题意M、N、P分别为其所在棱的中点，结合正方体的性质可知////,//BCADMNBDNP，由于BC平面MNP，MN平面MNP，所以//BC平面MNP；由于BD平面MNP，NP平面MNP，所以//BD平面MNP；由于BCBDB，所以平面//ACBD平面MNP，所以//A

B平面MNP，所以①正确.对于②，如图，设BC与DE相交于O，依题意M、N、P分别为其所在棱的中点，结合正方体的性质可知//ABON，因为ON与平面MNP相交，所以AB与平面MNP不平行，所以②错误.对于③，如图，设C是AD的中点，因为M是B

D的中点，所以//ABCM，而CM与平面MNP相交，所以AB与平面MNP不平行，所以③错误.对于④，如图，依题意M、N、P分别为其所在棱的中点，结合正方体的性质可知////ABCDNP，AB平面MNP，NP平面MNP，所以//AB平面MNP，所以④正确.综上所述，正确的序号有①④.故选

：B.5．（2020·济南大学城实验高级中学高一期中）如图，在下列四个正方体中，A、B为正方体的两个顶点，M、N、Q为所在棱的中点，则在这四个正方体中，直线AB不平行与平面MNQ的是（）A．B．C．D．【答案】D【解析

】对于A选项，如下图所示，连接CD，在正方体中，//ADBC且ADBC，所以，四边形ABCD为平行四边形，则//ABCD，NQ、Q分别为DE、CE的中点，则//NQCD，//ABNQ，AB平面MNQ，NQ平面M

NQ，//AB平面MNQ；对于B选项，连接CD，如下图所示：在正方体中，//ADBC且ADBC，所以，四边形ABCD为平行四边形，则//ABCD，M、Q分别为DE、CE的中点，则//MQCD，//ABMQ，AB平面MNQ，MQÌ

平面MNQ，//AB平面MNQ；对于C选项，连接CD，如下图所示：在正方体中，//ADBC且ADBC，所以，四边形ABCD为平行四边形，则//ABCD，M、Q分别为DE、CE的中点，则//MQCD，//ABMQ，

AB平面MNQ，MQÌ平面MNQ，//AB平面MNQ；对于D选项，如下图所示，连接BE交MN于点F，连接QF，连接CD交BE于点O，若//AB平面MNQ，ABÌ平面ABE，平面ABE平面MNQFQ，则//FQAB，则EFEQBEAE，由于四边形B

CED为正方形，对角线交于点O，则O为BE的中点，M、N分别为DE、CE的中点，则//MNCD，且MNBEF，则12EFENEOCE，1124EFOEBE，则14EFBE，又12EQAE，则EFEQBE

AE，所以，AB与平面MNQ不平行；故选：D.6．（2020·苏州新草桥中学高一期中）如图所示，在三棱柱ABC­111ABC中，E，F，G，H分别是AB，AC，11AB，11AC的中点，求证：（1）B，C，H，G四点共面；（2）1AE∥平面BCHG.【答案

】（1）证明见详解；（2）证明见详解；【解析】（1）∵G，H分别是11AB，11AC的中点，∴11//GHBC，而11//BCBC，∴//GHBC，即B，C，H，G四点共面.（2）∵E，G分别是AB，11AB的中点，∴1,AGEB平行且相等

，所以四边形1AEBG为平行四边形，即1//AEGB，又1AE面BCHG，GB面BCHG，∴1//AE面BCHG，7．（2020·湖南岳阳市·岳阳一中高一月考）如图，在三棱锥A﹣BCD中，AB⊥平面BCD，BC⊥BD，BC=3，BD=4，直

线AD与平面BCD所成的角为45°，点E，F分别是AC，AD的中点．（1）求证：EF∥平面BCD；（2）求三棱锥A﹣BCD的体积．【答案】（1）证明见解析；（2）8【解析】（1）∵点E，F分别是AC，AD的中点，∴EF

∥CD，又∵EF⊄平面BCD，CD⊂平面BCD，∴//EF平面BCD；（2）∵AB⊥平面BCD，∴∠ADB为直线AD与平面BCD所成的角，45,4ADBABBD，∵BC⊥BD，162BCDBCSBD,∴三棱锥A﹣BCD的体积183BCDVsAB．8．（2020·云南

高一期末）如图，在四棱锥PABCD中，PD平面ABCD，底面ABCD为梯形，//ABCD，60BAD，2PDADAB，4CD，E为PC的中点．（1）证明：//BE平面PAD；（2）求

三棱锥CBDE的体积．【答案】（1）证明见解析；（2）233.【解析】（1）设F为PD的中点，连结EF，FA，∵EF为PDC△的中位线，∴//EFCD，且122EFCD，又//ABCD，2AB，∴//ABEF，且ABEF，∴四边形ABEF是平行四边形，∴//B

EAF，又AF平面PAD，BE平面PAD，∴//BE平面PAD．（2）∵E是PC的中点，∴三棱锥12CBDEEBCDPBCDVVV，又ADAB，60BAD，∴ABD△是等边三角形，∴2BDABAD，D到AB的距离为3sin60232

AD，又4CD，∴143232BCDS△，∵PD平面ABCD，∴1143232333PBCDBCDVSPD△，∴三棱锥CBDE的体积12323CBDEPBCDVV．9．（2020·四川绵阳市

·高一期末）如图，在四棱柱1111ABCDABCD中，底面ABCD是平行四边形，1AA平面ABCD，3ADBD，32AB，E是1CD的中点.（1）证明：1//AD平面BDE；（2）若14AA，求三棱锥1DBDE的体积.【答案】（1）证明见解析；（2）3.【解析】（1）证明：连接AC交

BD于点O，连接EO.∵底面ABCD是平行四边形，∴点O为AC的中点.∵点E是棱1CD的中点，∴EO为1ACD△的中位线，∴1//EOAD，又EO平面BDE，1AD平面BDE，∴1AD∥平面BDE.（2）∵E是棱1CD的中点，∴点E到平

面BCD的距离等于点1D到平面BCD的距离的一半，∴点E到平面BCD的距离1114222dDD，∴三棱锥1DBDE的体积111133DBCDEBCDBCDBCDVVVSDDSd

△△，113BCDSDDd△113342332即三棱锥1DBDE的体积为3.【题组二面面平行】1．（2020·浙江杭州市·高一期末）已知直线a与平面,,，能使//的充分条件是（）①,②//,//③//,//aa④

,aaA．①②B．②③C．①④D．②④【答案】D【解析】对①，若,，垂直于同一个平面的两个平面可以相交，故①错误；对②，若//,//，则//，平面的平行具有传递性，故②正确；对③，若//,//aa，平行于同一直线的两平面可

以相交，故③错误；对④，,aa，垂直于同一直线的两平面平行，故④正确.综上：②④正确，故选：D.2．（2020·全国高一课时练习）如图，在下列四个正方体中，P，R，Q，M，N，G，H为所在棱的中点，则在这四个正方体中，阴影平面与PRQ所在平面平行的是（）A．B．C

．D．【答案】D【解析】由题意可知经过P、Q、R三点的平面即为平面PGRHNQ，如下图所示：对,BC选项：可知N在经过P、Q、R三点的平面上，所以B、C错误；对A：MC1与QN是相交直线，所以A不正确；对D：因为11AC

//RH，，1BC//QN，1111,ACBCC又容易知,RHQN也相交，111,ACBC平面11ACB；,RHQN平面PGRHNQ，故平面11ACB//平面PGRHNQ故选：D.3．（2020·江苏苏州市·常熟中学高一月考）已知m，n为两条不重合直线，，为两个不

重合平面，下列条件中，一定能推出//的是（）A．//mn，m，nB．//mn，m，nC．mn，//m，//nD．mn，m，n【答案】B【解析】只有一对直线平行，不能得出两平面平行

，A错，由//mn，m可得n，再由线面垂直的性质可得//，B正确；C中两平面,，没有任何关系，不能得出平行，C错；由mn，m，n可以得出，不能得出平行，D错．故选：B．【题组三平行的综合运用】1（2020·全国高一课时练习）（多选题）在正方体ABCD﹣A1B1C1D

1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：其中推断正确的序号是（）A．FG∥平面AA1D1D；B．EF∥平面BC1D1；C．FG∥平面BC1D1；D．平面EFG∥平面BC1D1【答案】AC【解析】在正方体1111ABCDABCD中，E，F，G分别是11A

B，11BC，1BB的中点，1//FGBC，11//BCAD，1//FGAD，FG平面11AADD，1AD平面11AADD，//FG平面11AADD，故A正确；11//EFAC，11AC与平面11BCD相交，

EF与平面11BCD相交，故B错误；E，F，G分别是11AB，11BC，1BB的中点，1//FGBC，FG平面11BCD，1BC平面11BCD，//FG平面11BCD，故C正确；EF与平面11BCD相交，平面EFG与平面11BCD相交，故D错误．

故选：AC．2．（2020·全国高一单元测试）（多选）如图是一几何体的平面展开图,其中四边形ABCD为正方形E,F,G,H分别为,,,PAPDPCPB的中点.在此几何体中,给出下列结论,其中正确的结论是（）A．平面//EFGH平面ABCDB

．直线//PA平面BDGC．直线//EF平面PBCD．直线//EF平面BDG【答案】ABC【解析】作出立体图形如图所示.连接,,,EFGH四点构成平面EFGH.对于A，因为E,F分别是,PAPD的中点,所以//EFAD.又EF平面ABCD，AD平面ABCD，所以/

/EF平面ABCD.同理,//EH平面ABCD.又EFEHE,EF平面EFGH,EH平面EFGH，所以平面//EFGH平面ABCD，故A正确；对于B，连接,,,ACBDDGBG，设AC的中点为M，则M也是BD的中点，所以//MGPA，又MG平面BDG,PA平面BDG，所以

//PA平面BDG，故B正确；对于C，由A中的分析知//EFAD，//ADBC，所以//EFBC，因为EF平面PBC，BC平面PBC，所以直线//EF平面PBC，故C正确；对于D，根据C中的分析可知//EFB

C再结合图形可得，BCBDB，则直线EF与平面BDG不平行，故D错误.故选：ABC3．（2021·全国高一课时练习）如图，在正方体1111ABCDABCD中，点E，F，G分别是11AB，11BC，1BB的中点，给出下列5个推断：①/

/FG平面11AADD；②//EF平面11BCD；③//FG平面11BCD；④平面//EFG平面11BCD；⑤平面//EFG平面11ACB.其中推断正确的序号是_________.【答案】①③⑤【解析】对于①，可知在正方体1111ABCDABCD中

，平面11//BBCC平面11AADD，且FG平面11BBCC，//FG平面11AADD，故①正确；对于②，E，F是11AB，11BC的中点，11//EFAC，11AC与平面11BCD相交，故EF与平面11BCD不平行，故②错误；

对于③，F，G是11BC，1BB的中点，1//FGBC，FG平面11BCD，1BC平面11BCD，//FG平面11BCD，故③正确；对于④，由②得EF与平面11BCD不平行，则平面EFG与平面11BCD不平行，故④错误；对于⑤，由①得11//EFAC，EF

平面11ACB，11AC平面11ACB，//EF平面11ACB，由③得//FG1BC，FG平面11ACB，1BC平面11ACB，//FG平面11ACB，EFFGF，平面//EFG平面11ACB，故⑤正确.故答案为：①③⑤.4．（2020·全国高一课时练习）如图，在棱长为2的正方

体1111ABCDABCD中，M是11AB的中点，点P是侧面11CDDC上的动点，且MP∥截面1ABC，则线段MP长度的取值范围是（）.A．[2,6]B．[6,22]C．[6,23]D．[6,3]【答案】B【解析】取CD的中点为N,1CC的中点为R,

11BC的中点为H,作图如下:由图可知,11//,MBNCMBNC,所以四边形1MNCB为平行四边形,所以1//MNBC,因为1111//,//MHACACAC,所以//MHAC,因为1,MNMHMACBCC,故平面

MNRH//平面1ABC,因为MP∥截面1ABC,所以MP平面MNRH,线段MP扫过的图形为MNR,由2AB知,22,2MNNR,在1RtMCR中,22211MRCRCM,即222156MR,所以6MR，所以222MN

NRMR,即MRN为直角,故线段MP长度的取值范围为,MRMN,即6,22,故选:B5．（2020·全国高一课时练习）如图，在棱长为1的正方体1111ABCDABCD中，点EF、分别是棱BC，1CC的中点，P是侧面11BCCB内一点，若

1AP//平面AEF，则线段1AP长度的取值范围是（）A．325(,)42B．325[,]42C．5[1,]2D．5[0,]2【答案】B【解析】如下图所示，分别取棱111,BBBC的中点M、N，连MN，1BC，∵,,,MNEF分别为所在棱的中点，则11,MN

BCEFBC，∴MN∥EF，又MN⊄平面AEF，EF⊂平面AEF，∴MN∥平面AEF．∵11,AANEAANE，∴四边形1AENA为平行四边形，∴1ANAE∥，又1AN平面AEF，AE⊂平面AEF，∴1AN∥平面AEF，又1ANMNN，∴平面1AMN∥平面AEF．∵P是侧面11BCCB内一

点，且1AP∥平面AEF，∴点P必在线段MN上．在11RtABM中，2221111151()22AMABBM．同理，在11RtABN中，可得152AN，∴1AMN为等腰三角形．当点P

为MN中点O时，1APMN，此时1AP最短；点P位于M、N处时，1AP最长．∵2222115232()()244AOAMOM，1152AMAN．∴线段1AP长度的取值范围是325[,]42．故选B．6．（2021·

全国高一课时练习）在正方体ABCD­A1B1C1D1中，E，F，G，H分别是BC，CC1，C1D1，A1A的中点．求证：（1）BF//HD1；（2）EG//平面BB1D1D．【答案】（1）证明见解析；（

2）证明见解析．【解析】证明：（1）如图所示，取BB1的中点M，连接MH，MC1，易证四边形HMC1D1是平行四边形，所以HD1∥MC1．又因为在平面BCC1B1中，BM//FC1，BM=FC1所以四边形BMC1F为平行四边形，所以MC1∥BF，所以BF∥HD1．（2）取BD的中点O，连接E

O，D1O，则OE∥DC且OE＝12DC，又D1G∥DC且D1G＝12DC，所以OE//D1G，OE=D1G所以四边形OEGD1是平行四边形，所以GE∥D1O．又D1O⊂平面BB1D1D，GE平面BB1D1D，所以EG∥平

面BB1D1D．7．（2020·全国高一课时练习）如图，三棱柱111ABCABC中，D，E，F分别为棱AB，BC，11CB中点.（1）求证：//AC平面1BDE；（2）求证：//AF平面1BDE.【答案】（1）证明见解析；（2）证明见解析.【解析】（1）在ABC中，D，E分别为棱A

B，BC中点.所以//DEAC，因为DE平面1BDE，AC平面1BDE，所以//AC平面1BDE.（2）在三棱柱111ABCABC中，11BCBC∥，因为E，F分别为BC，11CB中点，所以1CEBF∥，所以1BECF是平行四边形，所以

1//FCBE，因为FC平面1BED，1BE平面1BED，所以//FC平面1BDE，又因为//AC平面1BDE，ACCFC，所以平面//ACF平面1BDE，所以//AF平面1BDE.8．（2020·全国高一课时练习）已知正方体1111ABCDABCD中，P､Q分别为对角线B

D､1CD上的点，且123CQBPQDPD．（1）求证：//PQ平面11ADDA；（2）若R是AB上的点，ARAB的值为多少时，能使平面//PQR平面11ADDA？请给出证明．【答案】（1）证明见解析；（2）ARAB的值为35，证明见

解析．【解析】（1）连结CP并延长与DA的延长线交于M点，因为四边形ABCD为正方形，所以//BCAD，故~PBCPDM△△，所以23CPBPPMPD，又因为123CQBPQDPD，所以123CQCPQDPM，所以1//PQMD．又1MD平面11ADDA，PQ平面11ADDA，故

//PQ平面11ADDA．（2）当ARAB的值为35时，能使平面//PQR平面11ADDA．证明：因为35ARAB，即有23BRRA，故BRBPRAPD．所以//PRDA．又DA平面11ADDA，PR平面11A

DDA，所以//PR平面11ADDA，又PQPRP，//PQ平面11ADDA．所以平面//PQR平面11ADDA．【题组四线面、面面平行的性质】1．（2021·全国高一课时练习）如图，四棱锥PABCD的底面是边长为1的正方形，点E是棱PD上

一点，3PEED，若PFPC且满足//BF平面ACE，则______．【答案】23【解析】如图，连接BD，交AC于点O，连接OE，则BOOD，在线段PE取一点G使得GEED，则23PGPE.连

接,BGFG，则//BGOE，又因为OE平面AEC，BG平面AEC，所以//BG平面AEC.因为//BF平面ACE且满足BGBFB，故平面//BGF平面AEC.因为平面PCD平面BGFGF，平面PCD平面AECEC，则//GFEC.

所以23PFPGPCPE，即23为所求.故答案为：23.2．（2021·陕西省黄陵县中学高一期末）如图，梯形ABCD中，//BCAD，E是PD的中点，过BC和点E的平面与PA交于点F.求证：//BCEF.【答案】证明见解

析【解析】∵//BCAD，BC平面PAD，AD平面PAD，∴//BC平面PAD，∵BC平面BCEF，平面BCEF平面PADEF，∴//BCEF3．（2021·六盘山高级中学高一期末）如图所示，在四棱锥P

-ABCD中，BC//平面PAD，12BCAD，E是PD的中点.（1）求证：BC//AD；（2）求证：CE//平面PAB.【答案】（1）证明见解析；（2）证明见解析.【解析】证明：1在四棱锥PABCD中，//BC平面PAD，BC平面ABCD，平面ABCD平面PADAD

，//BCAD，2取PA的中点F，连接EF，BF，E是PD的中点，//EFAD，12EFAD，又由1可得//BCAD，且12BCAD，//BCEF，BCEF，四边形BCEF是平行四边形，//ECFB，EC平面PAB，FB平面P

AB，//EC平面PAB.4．（2020·六盘山高级中学高一月考）如图，在五面体ABCDEF中，四边形ABCD是矩形，求证：//ABEF.【答案】证明见解析【解析】因为四边形ABCD是矩形，所以//ABCD.因

为AB平面CDEF，CD平面CDEF，所以//AB平面CDEF.因为ABÌ平面ABFE，平面ABFE平面CDEFEF，所以//ABEF.5．（2020·浙江杭州市·高一期末）如图：S是平行四边形ABCD平面外一

点，M，N分别是SA，BD上的点，且AMDNSMNB，求证：//MN平面SBC【答案】证明见解析.【解析】过点N作//NGAD，交AB于G，连接MG，可得DBGAGBNN，又因为AMDNSMNB，所以SMBGAMAG，所以/

/MGSB，又因为MG不在平面SBC内，SB平面SBC，所以//MG平面SBC，又//BCAD，所以//BCNG，NG不在平面SBC内，GH平面SBC，//NG平面SBC，MGNGG，所以平面//SBC平面MNG，因为MN平面MNG，所以//MN平面SBC