【文档说明】2021年人教版高中数学必修第二册(精讲)6.3.2《平面向量数量积的坐标表示》（解析版）.doc，共(14)页，1.137 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38819.html

以下为本文档部分文字说明：

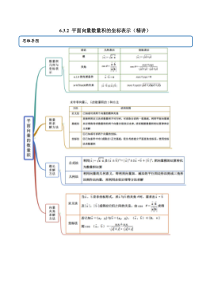
6.3.2平面向量数量积的坐标表示（精讲）思维导图常见考法考法一数量积的坐标运算【例1】（1）（2020·全国高一）向量2,3a，2,1br，则ab（）A．1B．1C．7D．0（2）（2020·全国高一）已知向

量(1,3)ar，(2,23)br，则a与b的夹角是（）A．6B．4C．3D．2（3）（2020·全国）已知2,1ar，11b,，则a在b上的投影的数量为（）A．22B．22C．55D．55（4）（2020·天津和平区·耀华中学高

一期末）已知向量(1,2)a，(3,1)bm，若ab，则m等于（）A．7B．5C．52D．12（5）（2020·黑龙江双鸭山市·双鸭山一中）设平面向量2,1ar，1,b，若a

与b的夹角为钝角，则的取值范围______.【答案】（1）B（2）C（3）B（4）D（5）11,,222U【解析】（1）因为2,3a，2,1br，所以22311ab

，故选：B.（2）设a与b的夹角为，则123231cos213412abab，又[0,180]，3，即a与b的夹角是3.故选：C（3）由题意知1ab，2b，ar在b上的投影的数量为122

2abb，故选：B.（4）因为ab，所以132+1=0abm，解得：12m，故选：D（5）因为a与b的夹角为钝角，0ab且不反向，2abrr，即20解得2当两向量反向时，存在0m使amb即2,1,mm，解得12

所以的取值范围11,,222U.故答案为：11,,222U.【一隅三反】1．（2020·银川市·宁夏大学附属中学高一期末）向量2112ab，，，，则2aba

（）A．1B．1C．6D．6【答案】D【解析】因为2112ab，，，所以23,0(2,1)3206abarrr故选：D2．（2020·广东高一期末）向量1,2ar，2,1br，则（）A．//abB

．abC．a与b的夹角为60°D．a与b的夹角为30°【答案】B【解析】∵向量1,2ar，2,1br，∴12210ab，∴ab.故选：B.3．（2020·湖北省汉川市第一高级中学高一期末）已知向量(0,23)

,(1,3)ab，则向量a在b上的投影为（）A．3B．3C．3D．3【答案】A【解析】因为向量(0,23),(1,3)ab，所以向量a在b上的投影为201233313abb故选：A4．（20

20·北京高一期末）已知向量4,2a，1,bm，若abrr，那么m的值为（）A．12B．12C．2D．2【答案】C【解析】向量4,2a，1,bm，若abrr，则0ab，即4120

m，解得2m.故选：C.5．（2020·沙坪坝区·重庆八中高一期末）已知(2,3)a，a与b的夹角为60，则a在b方向上的投影为（）A．72B．72C．27D．277【答案】A【解析】(2,3)a，a与b的夹角为60，||7a，7·cos602ababb，a在b

方向上的投影为72||abb．故选：A．6．（2020·湖南郴州市·高一月考）若向量2,1ar，1,1br，则向量ab与ab的夹角的余弦值为（）A．55B．55C．255D．255【答案】A【解析】

2,1,1,1ab，2,11,11,2ab，2,11,13,0ab，则1,23,03abab，5ab,3ab，

35cos553abababab.故选：A.7．（2020·河北唐山市·唐山一中高一月考）平面向量1,2a，4,2b，cmab（mR），且c与a的夹角与c与b的夹角互补，则m

（）A．2B．1C．1D．2【答案】A【解析】由已知(4,22)cmm，44458cos,55cammmcacacc，41644410cos,205cbmmmcbcbcc，∵c与a的夹角与

c与b的夹角互补，∴585mc41005mc，解得2m．故选：A．8．（2020·宝山区·上海交大附中高一期末）已知向量5,5a，,1b，若ab与ab的夹角是锐角，则实数的取值范围为______；【答案】7,11,7【解析】由

题意()()0abab，即220ab，2222551，∴77，若()abkab，则5(5)51(51)kk，解得321k，综上的范围是7,11,7．故答案为：7,11

,7．考法二巧建坐标解数量积【例2】（2020·四川高一期末）如图，边长为1的等边△ABC中，AD为边BC上的高，P为线段AD上的动点，则APBP的取值范围是（）A．[﹣316，0]B．[0，316]C．[﹣316，+∞）D．[﹣34，0]【答案

】A【解析】以D为坐标原点建立平面直角坐标系，如下所示：故可得310,,,022AB，设点0,Pm，因为点P在线段AD上，故可得30,2m.故APBP3130,,222mmmm

，故当34m时，取得最小值3334416，当0m或32时，取得最大值0.故APBP3,016.故选：A.【一隅三反】1．（2021·湖南）如图，直角梯形ABCD中，AB∥C

D，AB⊥AD，AB=AD=4，CD=8，若7CEDE，3BFFC，则AF·BE=_____.【答案】11【解析】以A为坐标原点，建立直角坐标系如图：因为直角梯形ABCD中，AB∥CD，AB⊥

AD，AB=AD=4，CD=8，若7CEDE，3BFFC所以(0,0)A，(4,0)B，(1,4)E，(5,1)F，所以(5,1)AF，(3,4)BE，则15411AFBE．故答案为：112．（2020·山东济

南市·）在ABC中，2BAC，2ABAC，P为ABC所在平面上任意一点，则PAPBPC的最小值为（）A．1B．12C．－1D．-2【答案】C【解析】如图，以,ABAC为,xy建立平面直角坐标

系，则(0,0),(2,0),(0,2)ABC，设(,)Pxy，(,)PAxy，(2,)PBxy，(,2)PCxy，(22,22)PBPCxy，∴22(22)(22)2222PAPBPCxxyyxxyy22112

()2()122xy，∴当11,22xy时，PAPBPC取得最小值1．故选：C．3．（2021·山西）已知正方形ABCD的边长为4，点E，F分别为CD，BC上的点，若13EAEB，13FAFD，则EF的最小值是（）A．1B．2C．10D．32【答案】B【

解析】如图所示，以AB为x轴，AD为y轴建立直角坐标系，设,4Ea，4,Fb，,0,4ab.故2,44,441613EAEBaaaa，故2430aa，故1a或3a.

24,4,441613FAFDbbbb，故2430bb，故1b或3b.22244EFab，当3,3ab时，EF有最小值为2.故选：B.考法三数量积与三角函数综合运用【例3】（2020·广东揭阳市·高一期末）已知向量sin,cosa

xx，3,1b，0,x.（1）若ab，求x的值；（2）记fxab，求fx的最大值和最小值以及对应的x的值.【答案】（1）6x；（2）23x时，fx取到最大值2，0x时，fx取到最小值1.【解析】（1）因为ab，所以sinco30s

bxxa，于是sintans33coxxx，又0,x，所以6x；（2）sin,3,1cosfxaxbx3sincosxx2sin6x.因为0,x，所以5,666x，从而12sin26x

于是，当62x，即23x时，fx取到最大值2；当66x，即0x时，fx取到最小值1.【一隅三反】1.向量(sin,2),(1,cos)ab，且ab，则2sin2co

s的值为（）A．1B．2C．12D．3【答案】A【解析】由题意可得sin2cos0ab，即tan2．∴222222sincoscos2tan1sin2cos1cossin1tan，故选A．2．（2020·

北京二十中高一期末）已知是锐角，1,1a，cos,sinb，且ab，则为（）A．30°B．45°C．60°D．30°或60°【答案】B【解析】∵1,1a，cos,sinb，且ab，∴coss

in0ab，求得cossin，tan1，由是锐角，所以45.故选：B.3．（2021·新疆）已知向量2,sinm,cos,1n,其中π0,2,且mn.(1)求sin2和cos2的值;(2)若10sin10,且π0

,2,求角.【答案】(1)4sin25，3cos25；(2)π4.【解析】(1)∵mn,∴2cossin0,即sin2cos.代入22cossin1,得25cos1,又π0,2

,则5cos5,25sin5.则5254sin22sincos2555.213cos22cos12155.(2)∵π0,2,π0,2,∴ππ

,22.又10sin10,∴310cos10.∴sinsin=sincoscossin=2531051025105102.由π0,2,得π4.4．（2021·江苏）已知

向量2,1sin(),2cosab，(1)若3=4，求证：ab;(2)若向量,ab共线，求b.【答案】(1)证明见解析；(2)28517.【解析】（1）当3=4时，2sin,2cossin,2cos,

22b又2,1a，2•21202abab（2）因为向量,ab共线，22cos1sinsin即sin4cos当cos0，则sin0与22sin+cos1矛盾，故舍去；当cos0时，由sin4

cos得：sintan4cos又22222222sin4cos=sin4cossin4cossincosb22tan420285tan11717

另解：由224sincos1sincos得2216sin=171cos17所以2220285=sin4cos1717b考法四数量积与几何的综合运用【例4】（2020·陕西渭南市·高一期末）已知向量3,4OA，

6,3OB，5,3OCmm.（1）若点A，B，C能够成三角形，求实数m应满足的条件；（2）若ABC为直角三角形，且A为直角，求实数m的值.【答案】（1）12m；（2）74m.【解析】（1）已知向量3,4OA，6,3OB

，5,3OCmm，若点A，B，C能构成三角形，则这三点不共线，即AB与BC不共线.3,1ABuuur，2,1ACmm，故知312mm，∴实数12m时，满足条件

.（2）若ABC为直角三角形，且A为直角，则ABAC，∴3210mm，解得74m.【一隅三反】1．（2020·唐山市第十一中学高一期末）已知2,1A，6,3B，0,5

C，则ABC的形状是（）．A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形【答案】A【解析】根据已知，有(8,4)AB，(2,4)AC，(6,8)BC，因为82(4)40ABAC，所以AB

AC，即90BAC．故ABC为直角三角形故选：A2．（2020·全国高一课时练习）已知(3,2)A、(2,1)B、(1,1)C且2APPB（1）证明：ABC是等腰直角三角形（2）求cos

APC．【答案】（1）证明见解析；（2）31010.【解析】（1）证明：由题意得(2,3)CA，(3,2)CB因为0CACB，所以CACB所以ABC是直角三角形又||4913CA，||9413CB，||||CACB，ABC是等腰直角三角形（2）解

：设点(,)Pxy，则(3,2)APxy，(2,1)PBxy2APPB，342xx且222yy，解得7x，0y，(7,0)P，(8,1)PC，(10,2)PA78PAPC，||65PC，||226P

A，78310cos1065226APC．3．（2020·全国高一课时练习）平面直角坐标系xOy中，已知向量(6,1),(,),(2,3)ABBCxyCD，且//ADBC．

（1）求x与y之间的关系式；（2）若ACBD，求四边形ABCD的面积．【答案】（1）20xy；（2）16.【解析】（1）由题意得(4,2)ADABBCCDxy，因为//ADBC，(,)BCxy，所以(4)(2)0xyyx

，即20xy，所以与y之间的关系式为：20xy①（2）由题意得(6,1)ACABBCxy，(2,3)BDBCCDxy，因为ACBD，所以(6)(2)(1)(3)

0xxyy，即2242150xyxy，②由①②得21xy或63.xy当21xy时，(8,0)AC，(0,4)BD，则1162ABCDSACBD四边形当63xy时，(0,4)AC，(

8,0)BD，则1162ABCDSACBD四边形所以，四边形ABCD的面积为16.