【文档说明】2021年人教版高中数学必修第二册(精讲)6.2.2《平面向量的数量积》（解析版）.doc，共(13)页，1.121 MB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38806.html

以下为本文档部分文字说明：

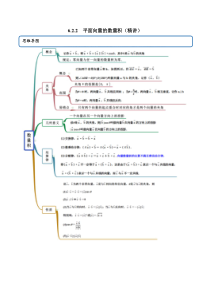
6.2.2平面向量的数量积（精讲）思维导图常见考法考法一向量的数量积【例1】（1）（2021·巴音郭楞蒙古自治州）已知||5a，||4b，a与b的夹角为60°，则ab________.（2）（2021·江苏高一）已知ABC是边长为6的正

三角形，求ABBC=____________（3）（2020·江西宜春市·高一期末）边长为2的菱形ABCD中，60BAD，E、F分别为BC，CD的中点，则AEEF【答案】（1）10（2）18（3）12【解析】（1

）1cos6054102abab.故答案为：10.（2）如图ABC是边长为6的正三角形，所以6ABBC，60ABC，所以1cos1806066182ABBCABBC，故答案

为：18（3）由题意画出示意图，如图，则111222AEEFABBEECCFABADADAB221111111422cos6044424422ADABADAB

.【一隅三反】1．（2020·全国高一）在ABC中，5AB，2BC，60B，则ABBC的值为（）A．53B．5C．53D．5【答案】D【解析】5AB，2BC，60B，()152cos180601052ABBC骣琪\?创

-=?=-琪桫.故选：D.2．（2020·全国高一）若2a，3b，则ab的最大值为________.【答案】6【解析】cos6cosabab，所以max()6ab.故答案为:63．（2020·福建泉州市·高一期末）平行四边形A

BCD中，4AB，22AD，34BAD，E是线段CD的中点，则AEAC（）A．0B．2C．4D．42【答案】C【解析】如图，根据题意：12AEADAB，ACADAB，且4AB，22AD，34BAD，22113132

()()816422()4222222AEACADABADABADABABAD．故选：C．4．（2021·江苏高一）在边长为1的等边三角形ABC中，M是边BC的中点，N是线段BM的中点，则AMAN（）A．34

B．34C．1D．1324【答案】B【解析】因为在边长为1的等边三角形ABC中，M是边BC的中点，N是线段BM的中点，所以12AMABACuuuruuuruuur，1113122444ANABAMABAB

ACABAC，因此22131131244244AMANABACABACABABACAC1313cos602444ABAC.故选：B.考法二向量的夹角【例2】（1）（2021·广东潮州）已知平面向量,ab，满

足25aab，且2,3ab，则向量a与向量b的夹角余弦值为（）A．1B．-1C．12D．-12（2）（2021·河南信阳市）若两个非零向量a，b满足2ababb，则向量ab与a的夹角

为()A．3B．23C．56D．6【答案】（1）C（2）D【解析】（1）平面向量,ab，满足25aab，且2,3ab，252cos,aabab，解得25221cos,232ab.故选：C

（2）∵非零向量a，b满足2ababb，∴平方得22abab，即2222||2||2abababab，则0ab，由2abb，平方得222||24||ababb，得223ab，即3ab则2abb

，22|3|abaaabb（），则向量ab与a的夹角的余弦值23||3223ababcosababb（），，0.6，，故选D.【一隅三反】1．（2021·胶州市）已知2ab，22abab，则a与b的夹角

为_________.【答案】60【解析】根据已知条件(2)()2abab，去括号得：222422cos242aabb，所以1cos0π2，，，60故答案为：602．（2021

·河南）若12,ee是夹角为60的两个单位向量，则122aee与1232bee的夹角为【答案】120°【解析】21211cos602eeee1212232abeeee221122176262,22eeee

222221211221||2444417,2aaeeeeee222221211221||329124912472bbeeeeee.设向量a与向量b的夹角为则712cos2||||77abab.又018

0剟，所以1203．（2021·陕西西安市）若两个非零向量a，b满足abab，则向量b与ab的夹角是______．【答案】56【解析】因为两个非零向量a，b满足abab，所以22aba，即2222aabba，所以22aba，22223aba

baabba，2232babbaab设向量b与ab的夹角为，则2332cos23babababab因为0,，所以56故答案为：56考法三向量的投影【例3】（1）（2

020·四川绵阳市·三台中学实验学校高一月考）已知向量2a，1b，且a与b的夹角为45，则a在b方向上的投影为（）A．2B．2C．3D．3（2）（2020·江西宜春市·高一期末）已知a，b为单位向量，2abab，则a在ab上的投影为（）A．13

B．263C．63D．223【答案】（1）B（2）C【解析】（1）因为向量2a，1b，且a与b的夹角为45所以2212||cos,21||abaabb，故选：B（2）因为a，b为单位向量，所以1abrr

，又2abab，所以222abab所以22222242aabbaabb，即121242abab，所以13ab，则2263abab，243aabaab，所以a在ab上的投影为4633263aabab.故选

：C.【一隅三反】1．（2020·合肥市第六中学高一月考）已知向量,ab的夹角为60，且2abrr，则向量ab在向量a方向上的投影为（）．A．1B．2C．3D．4【答案】A【解析】由题意，226co0sabaaabaab1

42222，所以向量ab在向量a方向上的投影为212abaa.故选：A.2．（2020·江西省崇义中学）设向量,ab满足2a，1b，且bab，则向量b在向量2ab上的投影的数量为()A．1B．1C．12D．12【答案】D【解析】bab,20a

bbabb,21abb.2221bababb,222442ababab,向量b在向量2ab上的投影的数量为2122babab.故选：D.3．（2020·全国高一专

题练习）设向量,ab满足||2a，||1b，且()bab，则向量b在向量2ab上的投影向量为（）A．eB．eC．12eD．12e【答案】D【解析】()bab，2()0babbab，1ab.2221()babbab

，22|2|442ababab.设与2ab方向相同的单位向量为e，向量b和向量2ab的夹角为，则向量b在向量2ab上的投影向量为(2)|2|(2)1||cos||2|||2|bbba

bbbbaeeeabaeb.故选:D.4．（2020·安徽蚌埠市·高一期末）设单位向量1e、2e的夹角为23，122aee，1223bee，则b在a方向上的投影为（）A．－332B．－3C

．3D．332【答案】A【解析】依题意得122111cos32eeurur，2221212122443aeeeeeerurururururur，22121212129223262abeeeeeeeerrururu

rururururur，因此b在a方向上的投影为933223baarrr，故选A.考法四向量的模长【例4】（2020·河北邢台市·）已知1a，3br，且向量a与b的夹角为60，则2ab

（）A．7B．3C．11D．19【答案】A【解析】因为1a，3br，a与b的夹角为60，所以2224424697aabbab，则27ab.故选：A.【一隅三反】1.（2020·台州市金清中学高一期末）已知2a，1b，a与

b的夹角为3，那么4ab等于【答案】23【解析】2222248168cos163abaabbaabb481612，423ab.2．（2020·四川省叙永县第一中学校高一期中）已知a、b满足：3a，2b，4ab，则ab__

_______.【答案】10【解析】222216ababab，因为3a，2b，所以32ab，所以22232942102ababab，可得10ab，故答案为：10.3．（2020·广东佛山市·高一期末）已知1a

，2b，则abab的最大值等于【答案】25【解析】因为1a，2b，所以222222252ababababab，当且仅当abab，即ab时取等号，4．（2020·浙江杭州市·

高一期末）若平面向量,,,abcd满足||1,||2,||3,()()4abbccdacbd，则||ad_________．【答案】14【解析】因为()()4acbd，所以4abbcbccd，所以

24abbcabcdbcbccd，因为2bc，所以24bc，所以0abbcabcdbccd，所以2adad2abbccd

222222abbccdabbcabcdbccd1492014.故答案为：14考法五平面向量运算的综合运用【例5-1

】（2020·黄梅国际育才高级中学高一期中）已知平面向量a，b，c，e，在下列命题中：①e为单位向量，且//ae，则aae；②//abrr存在唯一的实数R，使得ba；③若abbcrrrr且0brr，则ac；④a与b共线，b与c共线，则a与c共线；⑤2aaa.正确命题的

序号是（）A．①④⑤B．②③④C．①⑤D．②③【答案】C【解析】①因为e为单位向量，且//ae，所以aea，则aae，故①正确；②若0a，满足//abrr，但不能推出存在唯一的实数R，使得ba，故

②错误；③向量的数量积运算不满足消去律，故③错误；④若0b，则a与c不一定共线，故④错误；⑤由于2aaa，所以2aaa，故⑤正确．故选：C．【例5-2】（2020·全国高一）如图所示，半圆的直径6AB，O为圆心，C为半圆上不同于A、B的任意一点，若P

为半径OC上的动点，则PAPBPC的最小值为（）A．92B．4C．-5D．5【答案】A【解析】因为点O是线段AB的中点，所以向量2PAPBPO，所以2PAPBPCPOPC，又因为向量PO，PC方

向相反，所以2222626POPCPOPCPOPOPOPO2992322PO.故选：A.【一隅三反】1．（2020·北京朝阳区·人大附中朝阳学校高一期末）已知非零平面向量a，b，c，下列结论中正确的是（）（1）若acbc，则ab；（2）若

abab，则//ab（3）若abab，则ab（4）若0abab，则ab或abA．（1）（2）B．（2）（3）C．（3）（4）D．（2）（3）（4）【答案】B【解析】已知非零平面

向量a，b，c，（1）若acbc，则0abc，所以ab或abc，即（1）错；（2）若abab，则a与b同向，所以//ab，即（2）正确；（3）若abab，则222222abababab，所以20ab，则ab

；即（3）正确；（4）若0abab，则220ab，所以ab，不能得出向量共线，故（4）错；故选：B.2．（2020·湖北高一期末）已知两个非零向量a，b的夹角为23，且=2ab，则·ab的取值范围是（）A．2,03B．

2,0C．2,03D．1,0【答案】C【解析】因为2ab，所以2224aabb，所以2222cos43bbaa，即224aabb，由基本不等式的性质可知，222abab…，403ab

„，所以212·cos,0323ababab．故选：C．3．（2020·浙江杭州市·高一期末）已知向量,ab，满足||1,||2ab，若对任意模为2的向量c，均有||||27acbc，则向量,ab的夹角的取值范围是（）A．0

,3B．,3C．2,63D．20,3【答案】B【解析】由||1a，||2b，若对任意模为2的向量c，均有||||27acbc可得：()()27abcabcacbc

可得:()227ab,7ab平方得到2227abab，即1ab1cos1,cos,23abab故选：B4．（2020·浙江高一期末）设非零向量,ab的

夹角为，若2ab，且不等式2abab对任意恒成立，则实数的取值范围为（）A．1,3B．1,5C．7,3D．5,7【答案】A【解析】由题意，非零向量,ab的夹角为，且2ab，则2cos2cosab

abb，不等式2abab对任意恒成立，所以22(2)()abab，即22222442aabbaabb，整理得2(13)(84)cos0恒成立，因为cos1,1，所

以221384013840，即7315，可得13，即实数的取值范围为1,3.故选：A.