【文档说明】2021年人教版高中数学选择性必修第二册（精讲)拓展三《含参函数单调性的分类讨论》（解析版）.doc，共(9)页，727.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38170.html

以下为本文档部分文字说明：

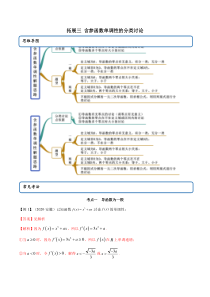
拓展三含参函数单调性的分类讨论考点一导函数为一根【例1】．（2020·安徽）已知函数3()fxxax.讨论()fx的单调性；【答案】见解析【解析】因为3fxxax，所以23fxxa.①当0a时，因为230fxxa，所以fx在R上单调

递增；②当0a时，令0fx，解得33ax或33ax.思维导图常见考法令0fx，解得3333aax，则fx在3,3a，3,3a上单调递增；在33,33aa

上单调递减.【一隅三反】1．（2020·河南）已知函数22exxxfax.讨论函数fx的单调性；【答案】答案见解析【解析】fx的定义域为R，2222e2e2exxxxxxafxax，当2a时，

0fx，则fx在R上是增函数；当2a时，2(2)e22exxxaxaxfax，所以02xfxa；02xfxa或2xa；022

fxaxa，所以fx在2,2aa上是减函数，在,2a和2,a上是增函数.2．（2020·山西运城）已知函数ln21fxxaxaR.讨论fx的单调性；【答案】具体见解析【解析】函数ln21fxxax

，定义域为0,，12fxax，当0a时，0fx.故fx在定义域0,上单调递增，此时无减区间.当0a时，令120fxax，得102xa；当10,2xa时，0fx，故fx单调递增；当1,2xa

时，0fx，故fx单调递减.综上所述，当0a时，fx在定义域0,上单调递增，此时无减区间；当0a时，fx在10,2a上单调递增，在1,2a

上单调递减.3．（2020·青海高二期末（理））已知函数，1()ln()fxaxaRx.讨论fx的单调性；【答案】当0a„时，()fx在(0,)上单调递减；当0a时，()fx在10,a上单调递减，在1,a上单调递增；【解析】因为

1()lnfxaxx，所以2211()(0)aaxfxxxxx.当0a„时，()0fx恒成立，()fx在(0,)上单调递减；当0a时，由()0fx，得10xa；由()0

fx，得1xa.故()fx在10,a上单调递减，在1,a上单调递增.综上，当0a„时，()fx在(0,)上单调递减；当0a时，()fx在10,a上单调

递减，在1,a上单调递增.考点二导函数为两根【例2】．（2020·四川南充·高二期末（理））已知函数22lnfxaxaxx，aR.（1）讨论fx的单调性；（2）若对任意0x，都有0fx成立，求实数a的取值范围.【答

案】（1）当0a时，在0,上，fx是减函数,当0a时，在10,a上，fx是减函数,在1,a上，fx是增函数；【解析】解：函数f（x）的定义域为（0，+∞）又

2/221211122axaxxaxfxaxaxxx当a≤0时，在（0，+∞）上，f′（x）＜0，f（x）是减函数当a＞0时，由f′（x）=0得：1xa或12x（舍）所以：在10a，上，f′（x）＜0，f（x）是减函数在1a

，上，f′（x）＞0，f（x）是增函数【一隅三反】1．（2020·赣州市赣县第三中学高二月考（文））已知函数21()ln()2fxxaxxaR，函数()23gxx．判断函数1()()()2Fxfxagx的单调性；

【答案】答案见解析【解析】由题意得2113()()()ln(1)222Fxfxagxxaxaxa，(0,)x；∴21(1)1(1)(1)()1axaxaxxFxaxxaxx．当0a时，()0Fx≥，函数()Fx在(0,)上单调

递增；当0a时，令()0Fx，有10xa：()Fx在10,a上单调递增；令()0Fx，有1xa：()Fx在1,a上单调递减；综上，当0a时，函数()Fx在(0,)上单调递增；当0a时，函数()yFx在

10,a上单调递增，在1,a上单调递减．2．（2020·河南郑州）已知函211()()().22xfxxeax讨论fx的单调性；（2）若fx有两个零点，求a的取值范围.【答案】答案见解析【解析】

1()22xfxxea.当0a时，令0fx，得1,2x，令0fx，得1,2x.故fx在1,2单调递减，在1,2单调递增.当0a时，令0fx，得112x，2ln

(2)xa.①当1ln(2)2a即2eae时，0fx，fx在R上单调递增.②当1ln(2)2a即02eae时，fx在1ln(2),2a上单调递减，在,ln2a

，1,2上单调递增.③当1ln(2)2a即2eae时，fx在1,ln(2)2a上单调递减，在1,2，ln(2)a,+上单调递增.3．已知函数321(1)32axxaxfx，讨论函数fx的单调性；【答案】见

解析【解析】因为321(1)32axxaxfx，所以2()(1)0fxxaxa.令()0fx，解得xa或1x.若1a，当0fx即1x或xa时，故函数()fx的单调递增区间为,1

,,a；当0fx即1xa时，故函数()fx的单调递减区间为1,a.若1a，则22()21(1)0fxxxx，当且仅当1x时取等号，故函数()fx在,上是增函数.若1a，当()0fx即xa或1x时，故函数()

fx的单调递增区间为,,1,a；当()0fx即1ax时，故函数()fx的单调递减区间为,1a.综上，1a时，函数()fx单调递增区间为(1)()a,,,+，单调递减区间为

(1,)a；1a时，函数()fx单调递增区间为(,)；1a时，函数()fx单调递增区间为()(1)a,,,+，单调递减区间为(,1)a.考点三不能因式分解【例3】．（2019·全国湖北·高二期中（文））设函数1()ln()fxxaxaRx讨论()fx的单调性；【

答案】答案见解析【解析】fx定义域为0,，22211'1axaxfxxxx，令221,4gxxaxa，①当22a时，0，'0fx，故fx在

0,上单调递增，②当2a时，，0gx的两根都小于零，在0,上，'0fx，故fx在0,上单调递增，③当2a时，，0gx的两根为221244,22aaaaxx，当10xx时，'0fx

；当12xxx时，'0fx；当2xx时，'0fx；故fx分别在120,,,xx上单调递增，在12,xx上单调递减.【一隅三反】1．（2019·洋县中学月考）已知函数2()ln2xfxxkx，其中Rk.（Ⅰ）若曲线()yfx在1x处的切线

与直线2xy平行，求实数k的值；（Ⅱ）讨论函数()fx的单调性；【答案】（Ⅰ）3k；（Ⅱ）答案见解析；【解析】（Ⅰ）1()0fxxkxx，∵曲线()yfx在1x处的切线与直线2x

y平行，∴(1)1f，即21k，故3k；（Ⅱ）函数()fx的定义域为(0,).当k2时，11()220fxxkxkkxx恒成立，故()fx在(0,)上单调递增；②当

2k时，211()xkxfxxkxx，令()0fx，得210xkx.∵240k，∴方程()0fx有两不等实根221244,22kkkkxx.∵120xxk，1210xx，

∴210xx.令()0fx，得10xx或2xx；令()0fx，得12xxx.综上所述，当k2时，()fx在(0,)上单调递增；当2k时，()fx在240,2kk

上单调递增，在2244,22kkkk上单调递减，在24,2kk上单调递增.另法（常规方法）：讨论24k的符号.当240k，即22k时，210xkx恒成立，则()0fx，()f

x在(0,)上递增；②当240k，即2k或2k时，方程()0fx有两不等实根12,xx.（i）当2k时，由12120,10xxkxx知120xx，则12()()()0xxxxfxx恒成立，故()fx在(0

,)上递增；（ii）当2k时，由12120,10xxkxx知210xx，令()0fx，得10xx或2xx；令()0fx，得12xxx.故()fx在1(0,)x、2(,)x上递增，在12(,)xx上递减.

综上，当k2时，()fx在(0,)上单调递增；当2k时，()fx在240,2kk上单调递增，在2244,22kkkk上单调递减，在24,2kk上单调递增.

2．已知函数221()ln()xfxaxaRx，讨论()fx的单调性；【答案】见解析【解析】()fx的定义域为(0,)，1()2lnfxxaxx21()2fxx2221axaxxx，对于22

10xax，28a，当[22,22]a时，()0fx，则()fx在(0,)上是增函数.当(,22)a时，对于0x，有()0fx，则()fx在(0,)上是增函数.当(22,)a时，令()0fx，得2804aax

或284aax，令()0fx，得228844aaaax，所以()fx在28(0,)4aa，28(,)4aa上是增函数，在2288(,)44aaaa上是减函数.综上，当(,22]a时，()fx在(0,)上是增函数；当(22,)

a时，()fx在28(0,)4aa，28(,)4aa上是增函数，在2288(,)44aaaa上是减函数.