【文档说明】2021年人教版高中数学选择性必修第二册（精讲)4.3《等比数列》（解析版）.doc，共(11)页，776.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38149.html

以下为本文档部分文字说明：

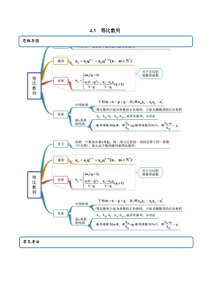
4.3等比数列思维导图常见考法考点一等比数列基本量计算【例1】（1）（2020·四川仁寿一中开学考试）在等比数列na中，126aa，33a，则公比q的值为（）A．12B．12或1C．－1D．12或－1（2）（2020·哈密市第十五中

学月考）已知各项均为正数的等比数列na的前4项和为15，且53134aaa，则3a（）A．16B．8C．4D．2（3）（2020·四川省内江市第六中学开学考试（理））等比数列na的前n项和131nnSa，则a=（）A．-1B．3C．-3D．1【答案】（1）B（2）C（3）

C【解析】（1）由题意112163aaqaq，解得131aq或11212aq．故选：B．【答案】C（2）设正数的等比数列{an}的公比为q，则2311114211115,34aaq

aqaqaqaqa，解得11,2aq，2314aaq，故选C．（3）因为数列是等比数列故满足2213aaa=，111aSa，232,6.aaaa代入2213aaa

=得到3.a故答案选C．【一隅三反】1．（2020·石嘴山市第三中学月考）已知na是等比数列，a1=2,a4=14,则公比q=（）A．12B．-2C．2D．12【答案】D【解析】∵na是等比数列，∴34111428aqa

，∴12q．故选：D．2．（2020·黑龙江工农·鹤岗一中高一期末（文））已知数列na满足112nnaa，若48a，则1a等于A．1B．2C．64D．128【答案】C【解析】因为数列na满足112nna

a，所以该数列是以12为公比的等比数列，又48a，所以188a，即164a；故选C.3．（2020·合肥市第十一中学高二开学考试）各项都是正数的等比数列na中，2311,,2aaa成等差数列，则公比q的值为（）A．512B

．512C．152D．512或512【答案】B【解析】由题得2231211112,,102aaaaqaaqqq，所以152q，因为na是各项都是正数的等比数列，所以0q，所以1+52q.故选：B4．（2020·全国高二月考（文）

）已知各项均为正数的等比数列na，且13213,,22aaa成等差数列，则4567aaaa的值是（）A．B．16C．D．19【答案】D【解析】各项均为正数的等比数列na的公比设为q，则q>0，由13213,,22aaa成等差数列，可得31232aaa，即211132aqaaq

，所以2230qq，解得3q或1q（舍），所以34344511565623267111119aaaqaqqqqaaaqaqqqqqq.故选：D.5．（2020·贵州省思南中学月考）设正

项等比数列{}na的前n项和为nS，10103020102(21)0SSS，则公比q等于（）A．12B．13C．14D．2【答案】A【解析】因为10103020102(21)0SSS，所以103020201020SSSS

所以302010201012SSSS，即102122301011122012aaaqaaa因为0na，所以12q故选：A考点二等比数列中项性质【例2】（1）（2020·自贡市田家炳中学开学考试）等比数列na的各项均为正数，且564718aaaa，

则3132310logloglogaaa（）A．12B．10C．8D．32log5（2）（2020·河南高二月考）在等比数列na中，若1358aaa，则42aa（）A．2B．4C．2D．4【答案】（1）B（2）B【解析】（1）由等比数列的性质可得：5647562

18aaaaaa，所以569aa.1102938479aaaaaaaa则5313231031103loglogloglog5log910aaaaa故选B.（2）由等比中项的性质可得

313538aaaa，解得32a，因此，2224324aaa.故选：B.【一隅三反】1．（2020·安徽滁州·期末）在等比数列{}na中，315,aa是方程2680xx的根，则1179aaaA．22B．2C．1D．2【答案】A【解析】由题得3153156,

8aaaa所以211798aaa，因为3153156080aaaa，所以315990,0,0,22.aaaa所以1179aaa82222.故答案为A2．（2019·福建高三学业考试）若三个数1，2，m成等比数列，则实数m（）A．8B．

4C．3D．2【答案】B【解析】因为1,2,m为等比数列，故212m即4m，故选：B.3．（2020·宁夏二模（理））已知实数1,,9m成等比数列，则椭圆221xym的离心率为A．63B．2C．63或2D．22或3【答案】A【解析】∵1，m，

9构成一个等比数列，∴m2=1×9，则m=±3．当m=3时，圆锥曲线2xm+y2=1是椭圆，它的离心率是23=63；当m=﹣3时，圆锥曲线2xm+y2=1是双曲线，故舍去，则离心率为63．故选A．考点三等比数列的前n项和性质【例3

】（2020·赣榆智贤中学月考）已知数列{an}是等比数列，Sn为其前n项和，若a1＋a2＋a3=4，a4＋a5＋a6=8，则S12=A．40B．60C．32D．50【答案】B【解析】由等比数列的性质可知，数列S3，S6−S3，S9−S6，S

12−S9是等比数列，即数列4,8，S9−S6，S12−S9是等比数列，因此S12=4＋8＋16＋32=60，选B．【一隅三反】1．（2020·赣榆智贤中学月考）已知na是各项都为正数的等比数列，nS是它的前n项

和，若47S，821S，则16S（）A．48B．90C．105D．106【答案】C【解析】由等比数列的性质得4841281612,,,SSSSSSS成等比数列，所以1216127,14,21,SSS成等比数列，所以121216162128,49,4956,105SSSS

.故选：C2．（2020·渝中·重庆巴蜀中学高一期中）等比数列na的前n项和为nS，若63:3:1SS，则93:SS（）A．4:1B．6:1C．7:1D．9:1【答案】C【解析】因为数列na为等比数列，则3S，63SS，96

SS成等比数列，设3Sm，则63Sm，则632SSm，故633SSS96632SSSS，所以964SSm，得到97Sm，所以937SS.故选：C.3．（2020·眉山市彭山区第一中学高二开学考试）若等比数列{an}的前n项和为Sn，且

S5＝10，S10＝30，则S20＝（）A．80B．120C．150D．180【答案】C【解析】因为数列na是等比数列，故可得510515102015,,,SSSSSSS依然成等比数列，因为51010,30SS，故可得10520

SS，故该数列的首项为10，公比为2，故可得420101215012S.故选：C.4．（2020·运城市景胜中学高二开学考试）设{}na是等比数列，且1231aaa，234+2aaa，则678aaa（）

A．12B．24C．30D．32【答案】D【解析】设等比数列na的公比为q，则2123111aaaaqq，232234111112aaaaqaqaqaqqqq，因此，

5675256781111132aaaaqaqaqaqqqq.故选：D.考点四等比数列的单调性【例4】（2020·上海市青浦高级中学高一期末）已知数列na满足156a，*11133nnaanN.（1）求证：数列1

2na是等比数列；（2）求数列na的通项公式.【答案】（1）证明见解析；（2）1123nna.【解析】（1）*11133nnaanN，111111111132332362111132222nnnnnnnnaaaaaaaa

，因此，数列12na是等比数列；（2）由于115112623a，所以，数列12na是以13为首项，以13为公比的等比数列，111112333nnna

，因此，1123nna.【一隅三反】1．（2020·湖北高一期末）已知{}na为等比数列，13527aaa，246278aaa，以nT表示{}na的前n项积，则使得nT达到最大值的n是（）A．4B．5C．6D．7【答案】A【解析】{}na为等比数列，31353

27aaaa，32464278aaaa，33a，432a，4312aqa，112a，543·14aaq．故{}na是一个减数列，前4项都大于1，从第五项开始小于1，以nT表示{}

na的前n项积，则使得nT达到最大值的n是4，故选：A．2．（2020·四川成都·高一期末（文））已知单调递减的等比数列na中，10a，则该数列的公比q的取值范围是（）A．1qB．0qC．1qD．01q【答案】D【解析】因为等比数列na单调递减，所以0q，11111110

nnnnnaaaqaqaqq，因为10a，所以110nqq，又因为1n，所以10,10nqq，所以01q，故选：D3．（2020·河北桃城·衡水中学高三月考（理））若na是公比为(0)qq的等比数列，记nS

为na的前n项和，则下列说法正确的是（）A．若na是递增数列，则10,0aqB．若na是递减数列，则10,01aqC．若0q，则4652SSSD．若1nnba，则nb是等比数列【答案】D【解析】A选项中，12,3aq，满足n

a单调递增，故A错误；B选项中，11,2aq，满足na单调递减，故B错误；C选项中，若111,2aq，则656554,aaSSSS，故C错误；D选项中，111(0)nnnnbaqbaq，所以nb是等比数列.故D正确.故选：D.4．（2020·宁夏兴庆·银川一中

期末）设等比数列na的公比为q，其前n项的积为nT，并且满足条件11a，9910010aa，99100101aa．给出下列结论：①01q；②9910110aa；③100T的值是nT中最大的；④使1nT成立的最大

自然数n等于198其中正确的结论是（）A．①③B．①④C．②③D．②④【答案】B【解析】①9910010aa，219711aq，9821()1qaq．11aQ，0q．又99100101aa，991a，且1001a．

01q，即①正确；②299101100100·01aaaa，9910101aa，即9910110aa，故②错误；③由于10099100TTa，而10001a，故有10099TT，故③错误；④中9919812198

119821979910099100()()()()1Taaaaaaaaaaa，199121991199219899101100()()()1Taaaaaaaaaa，故④正确．正确的为①④，故选：B．考点五证明判断等比数列【例5】

（2020·黑龙江省哈尔滨市双城区兆麟中学）已知正项数列na的前n项和为nS，若数列13logna是公差为1的等差数列，且22a是13,aa等差中项.（1）证明数列na等

比数列；（2）求数列na的通项公式.【答案】（1）证明见解析（2）13nna【解析】（1）因为数列13logna是公差为1的等差数列，所以11133loglog1nnaa，故113log1nnaa，所以13nnaa，所以数列

na是公比为3的等比数列.（2）因为22a是13,aa的等差中项，所以21322aaa，所以1112329aaa，解得11a，数列na的通项公式为-13nna.【一隅三反】1．（2020·玉龙纳西族

自治县田家炳民族中学高一月考）数列0,0,0,...,0,...（）A．既不是等差数列又不是等比数列B．是等比数列但不是等差数列C．既是等差数列又是等比数列D．是等差数列但不是等比数列【答案】D【解析】数列0,0,0,...,

0,...是无穷数列，从第二项开始起，每一项与它前一项的差都等于常数0，符合等差数列的定义，所以数列0,0,0,...,0,...是等差数列，根据等比数列的定义可知，等比数列中不含有为0的项，所以数列0,0,0,...,0,...不是等比数列，故选D.2．（2020·山

东省泰安第二中学高三月考）已知数列{}na是等比数列，那么下列数列一定是等比数列的是（）A．1{}naB．22log()naC．1{}nnaaD．12{}nnnaaa【答案】AD【解析】1na时，22log()0na，数列22{log()}na不一定是等比数列，1q

时，10nnaa，数列1{}nnaa不一定是等比数列，由等比数列的定义知1{}na和12{}nnnaaa都是等比数列．故选AD．3．（2020·浙江金华·期中）已知数列na满足11a，121nnnana．设nnabn．（1

）证明：数列nb为等比数列；（2）求na的通项公式．【答案】（1）详见解析；（2）12nnan．【解析】（1）121nnnana，nnabn，由条件可得121nnaann，即12nnbb，又111ba，所以nb是首项为1，公

比为2的等比数列．（2）由（1）可得12nnb，12nnan，所以12nnan．