【文档说明】2021年人教版高中数学选择性必修第三册6.2.1《排列及排列数》同步精讲（解析版）.doc，共(10)页，562.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-37470.html

以下为本文档部分文字说明：

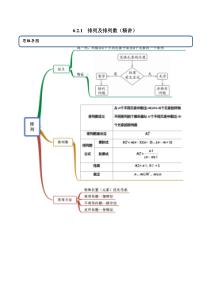
6.2.1排列及排列数（精讲）思维导图常见考法考点一排列的概念【例1】（2021年广东汕头）（1）下列问题是排列问题的是()A．从10名同学中选取2名去参加知识竞赛，共有多少种不同的选取方法？B．10个人互相通信一次，共写了多少封信？

C．平面上有5个点，任意三点不共线，这5个点最多可确定多少条直线？D．从1,2,3,4四个数字中，任选两个相加，其结果共有多少种？（2）从3个不同的数字中取出2个：①相加；②相减；③相乘；④相除；⑤一个为被开方数，一个为根指数．则上述问题为排列问题的个数为()A．2B．3C．4D．5【答

案】（1）B（2）B【解析】（1）排列问题是与顺序有关的问题，四个选项中只有B中的问题是与顺序相关的，其他问题都与顺序无关，所以选B.（2）排列与顺序有关，故②④⑤是排列．【一隅三反】1.（2020年广东河源）判断下列问题是否为排列问

题．(1)会场有50个座位，要求选出3个座位有多少种方法？若选出3个座位安排三位客人，又有多少种方法？(2)从集合M＝{1,2，„，9}中，任取两个元素作为a，b，可以得到多少个焦点在x轴上的椭圆方程x2a2＋y2b2＝1？可以得到多少个焦点在x轴上

的双曲线方程x2a2－y2b2＝1?(3)从1,3,5,7,9中任取3个数字，有多少种方法？若这3个数字组成没有重复的三位数，又有多少种方法？【答案】见解析【解析】(1)第一问不是排列问题，第二问是排列问题．“入座”问题

同“排队”问题与顺序有关，故选3个座位安排三位客人是排列问题．(2)第一问不是排列问题，第二问是排列问题．若方程x2a2＋y2b2＝1表示焦点在x轴上的椭圆，则必有a>b，a，b的大小关系一定；在双曲线x2a2－y2b2

＝1中，不管a>b还是a<b，方程x2a2－y2b2＝1均表示焦点在x轴上的双曲线，且是不同的双曲线，故是排列问题．(3)第一问不是排列问题，第二问是排列问题．从5个数中取3个数，与顺序无关；若这3个数组成不同的三位数，则与顺序有关．2.（2021年河北）下列问题是排列问题的是()A．从

8名同学中选取2名去参加知识竞赛，共有多少种不同的选取方法？B．10个人互相通信一次，共写了多少封信？C．平面上有5个点，任意三点不共线，这5个点最多可确定多少条直线？D．从1,2,3,4四个数字中，

任选两个相乘，其结果共有多少种？【答案】B【解析】排列问题是与顺序有关的问题，四个选项中只有B中的问题是与顺序有关的，其他问题都与顺序无关．故选B.考点二排列数【例2】（1）（2020·江苏省前黄高级中学）若220mA，则m（）A．5B．6C．7D．8（2）（2020·

永昌县第四中学）若532mmAA，则m的值为()A．5B．3C．6D．7（3）（2021·山西省长治市第二中学校高）不等式217nAn的解集为（）A．15nnB．1,2,3,4C．3,4D．4【答案

】（1）A（2）A（2）C【解析】（1）2(1)20mAmm,化解得2200mm解得：m=4（舍）或m=5故选：A（2）根据题意，若532mmAA，则有m（m﹣1）（m﹣2）（m﹣3）（m﹣4）=2×m（m﹣1）（m﹣2），即（m﹣3）（m﹣4）=2，解可得：m

=5故答案为A（3）由217nAn，得：127nnn，整理得2450nn，解得：15n，由题可知，12n且nN，则3n或4n，即原不等式的解集为：3,4.故选：C.【一隅三反】1．（2020·全国高

二单元测试）对于满足13n的正整数n，(5)(6)(12)nnn（）A．712nAB．75nAC．85nAD．125nA【答案】C【解析】根据排列数定义，要确定元素总数和选取个数，元素总数为5n，选取个数为(5)(12)18nn，85(5)(6)(12)nnnn

A.故选：C．2．（2020·宁夏育才中学）已知128934nnAA，则n（）A．5B．7C．10D．14【答案】B【解析】128934nnAA，可得387(82)4987(93)nn

，即3(11)(10)36nn，解得7n.故选：B.3．（2020·山东莱州一中）给出下列四个关系式：①(1)!!1nnn②11mmnnAnA③!()!mnnAnm④11(1)!()!mnnAmn其中正确的个数为（）A．1个B．2个C．3个D

．4个【答案】C【解析】①因为(1)!1121,!1221nnnnnnnn，故正确.②111!!,()!()!mmnnnnnAnAnmnm，故正确.③!()!mnnAnm，

正确.【方法总结】1.要注意mnA中隐含了3个条件：①m，*nN；②mn；③mnA的运算结果为正整数2.形11nnnnAnA，11nnnnnnnAAA（即!1!!nnnn），11mmmnnnAmAA的应用．④因

为!()!mnnAnm，所以11(1)!()!mnnAnm，故不正确.故选：C4．（1）解不等式288A6Axx；（2）证明：11AAAmmmnnnm.【答案】（1）x＝8；（2）详见解析.【解析】（1）由288A6Ax

x，得8!8!68!10!xx，化简得219840xx＋，解之得712x，①又820xx，2x8，②由①②及xN*得8x＝.（2111!!!1!!AA1A1!!!1!11!mmmnnnnnnn

nmnmmnmnmnmnmnmnmnm,11AAAmmmnnnm.考点三排队问题【例3】（2021·全国高二练习）有3名男生、4名女生，在

下列不同条件下，求不同的排列方法总数.(1)选5人排成一排；(2)排成前后两排，前排3人，后排4人；(3)全体排成一排，女生必须站在一起；(4)全体排成一排，男生互不相邻；(5)全体排成一排，其中甲不站最左边，也不站最右

边；(6)全体排成一排，其中甲不站最左边，乙不站最右边.【答案】（1）2520；（2）5040；（3）576；（4）1440；（5）3600；（6）3720.【解析】（1）从7人中选5人排列，共有57765432520A（种)．（2）分两步完

成，先选3人站前排，有37A种方法，余下4人站后排，有44A种方法，按照分步乘法计数原理计算可得一共有347476543215040AA（种).（3）捆绑法，将女生看成一个整体，进行全排列，有44A种，

再与3名男生进行全排列有44A种，共有4444576AA（种)．（4）插空法，先排女生，再在空位中插入男生，故有43451440AA（种)．（5）先排甲，有5种方法，其余6人有66A种排列方法，共有6653600A(种).（6）7名学生全排列，有77A种方法，其中甲在最左边时，有66A

种方法，乙在最右边时，有66A种方法，其中都包含了甲在最左边且乙在最右边的情形，有55A种方法，故共有76576523720AAA(种).【一隅三反】1．（2020·湖北高二期末）甲、乙、丙、丁四名同学和一名老师站成一排合影留念．若老师站在正中间，则不同站法的种数有（

）A．12种B．18种C．24种D．60种【答案】C【解析】根据题意，若老师站在正中间，则站法只有1种，将甲、乙、丙、丁全排列，安排在两边4个位置，有4424A种情况，由分步乘法计数原理知共有124=24

种，故选：C.2．（2020·山东淄博·高二期末）参加完某项活动的6名成员合影留念，前排和后排各3人，不同排法的种数为（）A．360B．720C．2160D．4320【答案】B【解析】分两步完成：第一步：从6人中选3人排前排：36120A种不同排法；【方法总结】排列常用方法1.简单问题直接法：

直接利用两个计数原理，直接进行排列组合解答.2.特殊元素(特殊位置)优先法：优先考虑一些特殊的元素和位置.3.相邻问题捆绑法：先把相邻元素捆绑在一起，再进行排列.4.不相邻问题插空法：先把没有位置要求的元素排列好，再排不相邻的元素.5.定序问题缩倍法（等概率问题缩倍法）先把所有的元素安排好，再

缩小一定的倍数.6.至少问题间接法：一般先考虑全部的排法，再排除不满足题意的排法.第二步：剩下的3人排后排：336A种不同排法，再按照分步乘法计数原理：1206720种不同排法，故选：B.3．（2020·湖北沙市中学高二月考）某单位有8个连在一起的车位，

现有4辆不同型号的车需要停放，如果要求剩余的4个车位中恰好有3个连在一起，则不同的停放方法的种数为（）A．240B．360C．480D．720【答案】C【解析】解法一：给8个车位编号：1，2，3，4，5，6，7，8，当1，2，3号车位停放3辆车时，有444A种停放方法；

当2，3，4号车位停放3辆车时，有443A种停放方法；当3，4，5号车位停放3辆车时，有443A种停放方法；当4，5，6号车位停放3辆车时，有443A种停放方法；当5，6，7号车位停放3辆车时，有443A种停放方法；当6，7，8号车位停放3辆车时，有444A种停放方法；所以不同的停放方法

的种数为44443444444344433334202024480AAAAAAA种.解法二：先定四个车位，其中三个车位连在一起捆绑，三个车位和另一个被四个空车位间隔开，四个空车位就1种排法，造成5个空格，排入三

个捆绑车位和一个车位有2520A种方法，再把4辆车停入四个车位有4424A种方法，根据乘法原理共有2024480种停车方法.故选：C.考点四数字问题【例4】（2021·天津静海一中）现有0、1、2、3、4、5、6、7、8、9共十个数字.（1）可以组成多少个无

重复数字的三位数？（2）组成无重复数字的三位数中，315是从小到大排列的第几个数？（3）可以组成多少个无重复数字的四位偶数？【答案】（1）648；（2）156；（3）2296；【解析】（1）由题意，无重复的三位数共有1299972648AA个

；（2）当百位为1时，共有299872A个数；当百位为2时，共有299872A个数；当百位为3时，共有118412AA个数，所以315是第727212156个数；（3）无重复的四位偶数，所以个位必须为0,2,4,6,8，千

位上不能为0，当个位上为0时，共有39504A个数；当个位上是2,4,6,8中的一个时，共有1218841792AAA个数，所以无重复的四位偶数共有50417922296个数；【一隅三反】1．（2020·浙江省东阳中学）由0，1，2，3，4，5共6个不

同数字组成的6位数，要求0不能在个位数，奇数恰好有2个相邻，则组成这样不同的6位数的个数是（）A．144B．216C．288D．432【答案】B【解析】先从3个奇数中选出2个捆绑内部全排共有236A种排

法，再把捆绑的2个奇数看成一个整体，因为这个整体与剩下的一个奇数不相邻，将2个非0偶数全排有222A种选法，奇数插空全排有236A种选法，最后把0插空，0不能在两端，有3种排法，可组成这样不同的6

位的个数为6263216种排法，故选：B2．（2020·福建省福州外国语学校用数字0,1,2,3,4,5组成没有重复数字的五位数，其中比40000大的偶数共有A．144个B．120个C．96个D．72个【答案】B【解析】根据题意，符合条件的五位数

首位数字必须是4、5其中1个，末位数字为0、2、4中其中1个；分两种情况讨论：①首位数字为5时，末位数字有3种情况，在剩余的4个数中任取3个，放在剩余的3个位置上，有A43=24种情况，此时有3×24=72个，②首位数字

为4时，末位数字有2种情况，在剩余的4个数中任取3个，放在剩余的3个位置上，有A43=24种情况，此时有2×24=48个，共有72+48=120个．故选B3．（2021·湖北车城高中）用数字0，1，2，3，4，5组成没有

重复数字的四位数.（1）可组成多少个不同的四位数？（2）可组成多少个不同的四位偶数？【答案】（1）300；（2）156.【解析】（1）根据题意分步完成任务：第一步：排千位数字，从1，2，3，4，5这5个数字中选1个来排，有155A种不同排法；第二步：排百位、十位、个位数字，从排了千位

数字后剩下的5个数字中选3个来排列，有3554360A种不同排法；所以组成不同的四位数有560300种，（2）根据题意分类完成任务：第一类：个位数字为0，则从1，2，3，4，5这5个数字中选3个来排在千位、百位、十位，有3554360A种不同排法；第二类：个位数字为2或4，则

0不能排在千位，有112244244396AAA种不同排法；所以组成不同的四位偶数有6096156种.