【文档说明】（通用版）中考数学一轮复习练习卷5.1《平行四边形与多边形》课后练习（含答案）.doc，共(11)页，149.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-35512.html

以下为本文档部分文字说明：

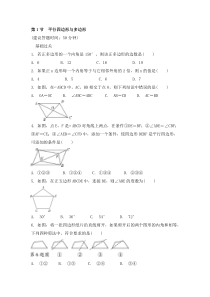
第1节平行四边形与多边形(建议答题时间：50分钟)基础过关1.若正多边形的一个内角是150°，则该正多边形的边数是()A.6B.12C.16D.182.如果正n边形每一个内角等于与它相邻外角的2倍，则n的值是()A.4B.5C.6D.73.如图，在▱ABCD中，AC，BD相交于点

O，则下列结论中错误的是()A.OA＝OCB.∠ABC＝ADCC.AB＝CDD.AC＝BD4.如图，点E，F是▱ABCD对角线上两点，在条件①DE＝BF；②∠ADE＝∠CBF；③AF＝CE；④∠AEB＝∠CFD中，添加一个条件，使四边形DEBF是平行四边形，可添加的条件是()A.①②③B

.①②④C.①③④D.②③④5.如图，在正五边形ABCDE中，连接BE，则∠ABE的度数为()A.30°B.36°C.54°D.72°6.如图，将一张四边形纸片沿直线剪开，如果剪开后的两个图形的内角和相

等，下列四种剪法中，符合要求的是()A.①②B.①③C.②④D.③④7.如图，在平行四边形ABCD中，AE平分∠DAB，∠AED＝26°，则∠C的度数为()A.26°B.42°C.52°D.56°8.如图，在▱ABCD中，连接AC，∠ABC＝∠CAD＝45°，AB＝

2，则BC的长是()A.2B.2C.22D.49.如图，▱ABCD的对角线AC与BD相交于点O，AE⊥BC，垂足为E，AB＝3，AC＝2，BD＝4，则AE的长为()A.32B.32C.217D.221710.如图，EF过▱ABCD对角线的交点

O，交AD于E，交BC于F，若▱ABCD的周长为18，OE＝1.5，则四边形EFCD的周长为()A.14B.13C.12D.1011．五边形的内角和为________．12．在▱ABCD中，若∠B＋∠D＝200°，则∠A＝_____

___°.13.如图，在▱ABCD中，对角线AC，BD相交于点O，点E是AB的中点，OE＝5cm，则AD的长为________cm.14．如图，在▱ABCD中，∠D＝100°，∠DAB的平分线AE交DC于点E，连接BE，若AE＝AB，则∠EBC的度数为________．

15.如图，在▱ABCD中，AE⊥BC于点E，AF⊥CD于点F，若∠EAF＝56°，则∠B＝________.16.如图，在▱ABCD中，延长AB至点E，延长CD至点F，使得BE＝DF.连接EF，与对角线AC交于点O.求证

：OE＝OF.17.如图，四边形ABCD是平行四边形，E、F是对角线BD上的两点，且BF＝ED，求证：AE∥CF.18.如图，点B，E，C，F在一条直线上，AB＝DF，AC＝DE，BE＝FC.(1)求证：△ABC≌△DFE；(2)连接AF，BD，求证：四边形ABDF是平行四边形．19.如图，四边形

ABCD中，AC、BD相交于点O，O是AC的中点，AD∥BC，AC＝8，BD＝6.(1)求证：四边形ABCD是平行四边形；(2)若AC⊥BD，求▱ABCD的面积．20.如图，在平行四边形ABCD中，AE⊥BC，CF⊥AD

，垂足分别为E、F，AE、CF分别与BD交于点G和H，且AB＝25.(1)若tan∠ABE＝2，求CF的长；(2)求证：BG＝DH.满分冲关1.在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4两部分，则平行四边形ABCD周长是()A.2

2B.20C.22或20D.182.如图，在▱ABCD中，对角线AC，BD相交于点O.若AB＝4，BD＝10，sin∠BDC＝35，则▱ABCD的面积是__________．3.如图，在▱ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，且CG＝2BG，S△BPG＝1，则S▱AEPH＝__

______．4.如图，四边形ABCD是平行四边形，AD＝AC，AD⊥AC，E是AB的中点，F是AC延长线上的一点．(1)若ED⊥EF，求证：ED＝EF；(2)在(1)的条件下，若DC的延长线与FB交于点P，试判定四边形ACPE是

否为平行四边形？并证明你的结论(请先补全图形，再解答)；(3)若ED＝EF，ED与EF垂直吗？若垂直给出证明，若不垂直说明理由．答案基础过关1.B【解析】设多边形的边数为n，根据正多边形内角和公式可得(n－2)

×180°＝n×150°，解得n＝12.2.C【解析】设该正n边形的一个外角为x，则与它相邻的内角为2x，根据题意得，2x＋x＝180°，解得x＝60°，∵多边形的外角和为360°，∴n＝360°÷60°＝6.3.D【解析】∵四边形ABCD是平行四边形，∴AO＝CO，∠AB

C＝∠ADC，AB＝CD，∴A，B，C选项都正确，而AC与BD不一定相等．4.D【解析】由平行四边形的判定方法可知：若是四边形的对角线互相平分，可证明这个四边形是平行四边形，①不能证明对角线互相平分，

只有②③④可以．5.B【解析】∵五边形ABCDE是正五边形，∴∠A＝180°×（5－2）5＝108°，∵AB＝AE，∴∠ABE＝∠AEB＝12(180°－∠A)＝36°.6.B【解析】要使得两个多边形的内角和相等，则这两个多边形的边数应该相同，故①和③符合条件．7.C【解析】∵平行

四边形ABCD，∴CD∥AB，∴∠AED＝∠EAB，∴∠EAB＝26°，∵AE平分∠DAB，∴∠DAB＝52°，∴∠C＝52°.8.C【解析】∵四边形ABCD为平行四边形，∴AD∥BC，∴∠ACB＝∠CAD，又∵∠

ABC＝∠CAD＝45°，∴∠ACB＝∠ABC＝∠CAD＝45°，∴∠BAC＝180°－45°－45°＝90°，AB＝AC，∵在Rt△ABC中，AB＝AC＝2，∴BC＝AB2＋AC2＝22＋22＝22.9.D【解析】

∵四边形ABCD是平行四边形且AC＝2，BD＝4，∴AO＝OC＝1，BO＝OD＝2，又∵AB＝3，∴AB2＋AO2＝BO2，∴∠BAO＝90°，在Rt△BAC中，BC＝AB2＋AC2＝（3）2＋22＝7，∵S△ABC＝12AB·AC

＝12BC·AE，∴AE＝AB·ACBC＝3×27＝2217.10.C【解析】∵四边形ABCD是平行四边形，∴OA＝OC，AD∥BC，∴∠DAC＝∠ACB，在△OAE和△OCF中，∠DAC＝∠ACBOA＝OC∠AOE＝∠COF，∴△OAE≌△OCF，∴CF＝A

E，OE＝OF，∵OE＝1.5，∴EF＝2OE＝3，∵▱ABCD的周长为18，∴AD＋DC＝9，∴四边形EFCD的周长＝DE＋EF＋CF＋CD＝DE＋AE＋CD＋EF＝AD＋CD＋EF＝9＋3＝12.11.540°【解析】由n边形的内角和为(n－

2)×180°可知，五边形的内角和为(5－2)×180°＝3×180°＝540°.12.80【解析】在▱ABCD中，∠B＝∠D，∵∠B＋∠D＝200°，∴∠B＝100°，∵AD∥BC，∴∠A＋∠B＝180°，∴∠A＝80°.13.10【解析

】∵点O和点E分别是边BD和BA的中点，∴OE是△BAD的中位线，即OE＝12AD＝5cm，∴AD＝10cm.14.30°【解析】∵在▱ABCD中，∠D＝100°，AB∥DC，∴∠ABC＝∠D＝100°，∴∠

AED＝∠BAE,∵AE平分∠DAB，∴∠AED＝∠BAE＝∠DAE＝40°，又∵AE＝AB，∴∠ABE＝70°，∴∠EBC＝30°.15.56°【解析】在四边形AECF中，有两个内角是直角，根据“四边形内角和等于360°”得∠EAF＋∠C＝180°，又因为四边形ABCD是平行四边形，所以∠B＋∠

C＝180°，所以∠B＝∠EAF＝56°.16.证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∵BE＝DF，∴AB＋BE＝CD＋DF，即AE＝CF.∵AB∥CD，∴AE∥CF，∴∠E＝∠F，∠CAB＝∠ACD，∴△AOE≌△COF(ASA)，∴OE＝OF.17.证明：∵四边形ABC

D是平行四边形，∴AD∥BC，且AD＝BC，∴∠ADE＝∠CBF，又∵BF＝ED，∴△AED≌△CFB(SAS)，∴∠AED＝∠CFB，∴AE∥CF.18.证明：(1)∵BE＝FC，∴BC＝FE.在△A

BC和△DFE中，AB＝DFAC＝DEBC＝FE，∴△ABC≌△DFE(SSS)；(2)如解图，连接AF，BD，由(1)知△ABC≌△DFE，第18题解图∴∠ABC＝∠DFE，∴AB∥DF，又∵AB＝DF，∴四边形ABDF是平行四边形．19.(1

)证明：∵O是AC的中点，∴OA＝OC，∵AD∥BC，∴∠ADO＝∠CBO，在△AOD和△COB中，∠ADO＝∠CBO∠AOD＝∠COBOA＝OC，∴△AOD≌△COB(AAS)，∴OD＝OB，∴四边形ABCD是平行四边形；(2)解：∵四边形ABCD是平行四边形，AC⊥

BD，∴四边形ABCD是菱形，∴▱ABCD的面积是12AC·BD＝24.20.(1)解：∵AE⊥BC，CF⊥AD，AD∥BC，∴AE＝CF，∵tan∠ABE＝2＝AEBE，∴BE＝12AE，∴AB＝AE2＋BE2＝52AE，即AB∶AE＝5∶2，∵AB＝25，∴CF＝AE＝2×255＝4；(

2)证明：∵四边形ABCD是平行四边形，∴AB＝CD且AB∥CD，∠ABE＝∠CDF，∴∠ABD＝∠BDC，∵AE⊥BC，CF⊥AD，∴∠ABE＋∠BAE＝∠CDF＋∠DCF＝90°，∴∠BAE＝∠DCF,∴△ABG≌△CD

H(ASA)，∴BG＝DH.满分冲关1.C【解析】如解图，在平行四边形ABCD中，AD∥BC，则∠DAE＝∠AEB.∵AE平分∠BAD，∴∠BAE＝∠DAE，∴∠BAE＝∠BEA，∴AB＝BE，BC＝BE＋EC，①当BE＝3，EC＝4时，平行四边形ABCD的周长为：2(

AB＋AD)＝2×(3＋3＋4)＝20.②当BE＝4，EC＝3时，平行四边形ABCD的周长为：2(AB＋AD)＝2×(4＋4＋3)＝22.第1题解图2.24【解析】如解图，过点C作CE⊥BD交BD于点E，在▱ABCD中，AB＝4可得CD＝AB＝4，再由sin∠BD

C＝35得CECD＝35，即CE4＝35，所以CE＝125，所以S△BDC＝12BD·CE＝12×10×125＝12，则S▱ABCD＝2S△BDC＝12×2＝24.第2题解图3.4【解析】由四边形ABCD是平行四边形，可得AB∥CD，AD∥BC，又知EF∥BC，GH∥AB，因而得到四边形

BEPG、四边形GPFC、四边形PHDF、四边形AEPH都是平行四边形．∵BD、BP、DP分别是平行四边形ABCD、平行四边形BEPG、平行四边形PHDF的对角线，根据平行四边形的对角线将平行四边形分成两个全等的三角形．得到S△ABD＝S△CBD，S△PHD＝S△PFD，S△BPG＝S△

BPE，从而得出S四边形AEPH＝S四边形GPFC，又∵CG＝2BG，∴S四边形AEPH＝S四边形GPFC＝2S四边形BGPE＝4S△BPG＝4.4.(1)证明：在▱ABCD中，∵AD＝AC，AD⊥AC.∴AC＝BC，AC⊥BC，第4题解图如解图，连接CE，∵E为AB中点，∴AE＝EC.∴∠

ACE＝∠BCE＝45°，∴∠DAE＝∠ECF＝135°，又∠AED＋∠CED＝∠CEF＋∠CED＝90°，∴∠AED＝∠CEF，∴△AED≌△CEF(ASA)，∴ED＝EF；(2)解：∵△AED≌△CEF，∴AD＝CF，∴AC＝CF，又C

P∥AE，∴CP为△FAB的中位线，∴CP＝12AB＝AE，∴四边形ACPE是平行四边形；(3)解：垂直；证明：过点E作EH⊥AF于H，作EG⊥DA交DA延长线于点G，∵AE＝EC，∴∠EAC＝∠HCE＝45°，∴△AGE≌△CH

E，∴EG＝EH，又ED＝EF，∴Rt△DEG≌Rt△FEH，∴∠ADE＝∠CFE，∴∠DEA＝∠FEC，∴∠FEC＋∠DEC＝∠DEA＋∠DEC＝90°，∴∠DEF＝90°，∴ED⊥EF.