【文档说明】苏科版九年级数学上册第2章 第20讲圆周角的应用课后练习(含答案).doc，共(3)页，78.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-47364.html

以下为本文档部分文字说明：

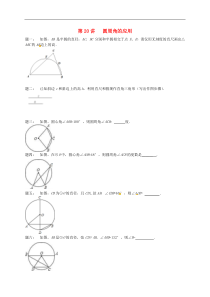
第20讲圆周角的应用题一：如图，AB是半圆的直径，AC、BC分别和半圆相交于点E、D，请仅用无刻度的直尺画出△ABC的AB边上的高．题二：已知斜边c和斜边上的高h，利用直尺和圆规作直角三角形（写出作图步骤）．题三：如图，圆心角∠AOB=1

00°，则圆周角∠ACB=度．题四：如图，在⊙O中，圆心角∠AOB=48°，则圆周角∠ACB的度数是______.题五：如图，CD为⊙O的直径，且CD⊥弦AB，∠CDB=60°，则∠AOD=．题六：如图，AB是⊙O的直径，弦CD∥AB，∠AOD=

132°，则∠B=.第20讲圆周角的应用题一：见详解．详解：如图所示：①连接AD、BE，因为AB是半圆的直径，所以∠AEB=∠ADB=90°，所以AD、BE分别是边BC和AC上的高，②设AD、BE相交于点M，连接CM并延长交AB

于点H，③CH即为所求的△ABC的AB边上的高(根据三角形的三条高线交于一点)．题二：见详解．详解：如图所示：①作射线AD，在射线上截取AB=c，②以AB为直径作半圆，③作AB的平行线l，使两平行线相

距h，④直线l与半圆的交点即为直角三角形的顶点C，⑤连接BC、AC，△ABC即为所求的直角三角形．题三：130.详解：在优弧AB上取点D（不与A、B重合），连接AD、BD；则∠ADB=12∠AOB=12×100°=50°；∵四边形ADBC内接于⊙O，∴∠ACBADB题四：24°．详解：根据一条

弧所对的圆周角等于它所对的圆心角的一半，得∠ACB=12∠AOB=24°．题五：60°．详解：∵CD⊥弦AB，且∠CDB=60°，∴∠B，∵CD为⊙O的直径，∠AOD为圆心角，题六：∵∠AOD=132°，∴∠BOD=48°，∴∠BCD=12∠BOD=24°，∵CD∥AB，∴

∠B=∠BCD=24°．