【文档说明】2022年中考数学二轮复习专题《相似三角形的综合应用》练习册 (含答案).doc，共(19)页，217.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-41852.html

以下为本文档部分文字说明：

第7课时相似三角形的综合应用类型一A字型(有一个公共角)1.(2016昆明)如图，反比例函数y＝kx(k≠0)的图象经过A、B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，

连接BO交AC于点E，若OC＝CD，四边形BDCE的面积为2，则k的值为________．第1题图2.(2016锦州)如图，已知△ABC，∠ACB＝90°，AC<BC，点D为AB的中点，过点D作BC的垂线，垂足为点F，过点A、C、D作⊙O交BC于点E，连接CD、DE.(1

)求证：DF为⊙O的切线；(2)若AC＝3，BC＝9，求DE的长．第2题图类型二8字型(有一组对顶角)3.(2016抚顺)如图，矩形ABCD的顶点D在反比例函数y＝kx(x＜0)的图象上，顶点B、C在x轴上，对角线AC的延长线交y轴于点E，

连接BE，若△BCE的面积是6，则k的值为()A.－6B.－8C.－9D.－12第3题图4.(2017眉山)如图，点E是正方形ABCD的边BC延长线上一点，连接DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交DC于G.(1)求证：BG＝DE;(2)若点G为CD的中点，求HGGF的值．第

4题图类型三母子型(有一个公共角，及一边共用)∠A公共角，AC为公共边∠ACD＝∠B或∠ADC＝∠ACB5.(2015上海)已知：如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE＝OB，连接DE.(1)求证：DE⊥BE；(2)如果OE⊥

CD，求证：BD·CE＝CD·DE.第5题图6.(2016成都)如图，在Rt△ABC中，∠ABC＝90°，以CB为半径作⊙C，交AC于点D，交AC的延长线于点E，连接BD，BE.(1)求证：△ABD∽△AEB；(2)当ABBC＝43时，求tanE;(3)在(

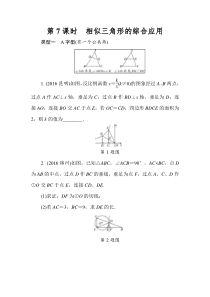
2)的条件下，作∠BAC的平分线，与BE交于点F，若AF＝2，求⊙C的半径．第6题图类型四双垂直型△ACD∽△CBD∽△ABC7.如图，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于点E.(1)求证：△ABD∽△CBE；(2)若BD＝3，

BE＝2，求AC的长．第7题图8.(2015陕西)如图，AB是⊙O的直径，AC是⊙O的弦，过点B作⊙O的切线DE，与AC的延长线交于点D，作AE⊥AC交DE于点E.(1)求证：∠BAD＝∠E；(2)若⊙O的半径为5，AC＝8，求BE的长．第8题图类型五一线三等角型（

∠1＝∠2＝∠3）阴影部分两三角形相似9.(2017宿迁)如图，在△ABC中，AB＝AC，点E在边BC上移动(点E不与点B、C重合)，满足∠DEF＝∠B，且点D、F分别在边AB、AC上．(1)求证：△BDE∽△CEF;(2)当点E移动到BC的中点时，求证：FE平分∠DFC.第9题图

10.如图，等边△ABC的边长为6，点D，E，F分别在BC，AB，AC上，且∠EDF＝60°.(1)求证：△BDE∽△CFD;(2)当BD＝1，CF＝3时，求BE的长．第10题图类型六三垂直型11.(2017江西)如图，正方形ABC

D中，点E，F，G分别在AB，BC，CD上，且∠EFG＝90°.求证：△EBF∽△FCG.第11题图12.如图，∠AOB＝90°，反比例函数y＝kx的图象过点B，若点A的坐标为(2，1)，BO＝25，求

B的坐标和反比例函数的解析式．第12题图13.(2016达州)如图，已知AB为半圆O的直径，C为半圆O上一点，连接AC，BC，过点O作OD⊥AC于点D，过点A作半圆O的切线交OD的延长线于点E，连接BD并延长交AE于点F.(1)求证：AE·BC＝AD·AB；(2

)若半圆O的直径为10，sin∠BAC＝35，求AF的长．第13题图答案1.－163【解析】∵AC⊥x轴，BD⊥x轴，∴AC∥BD，∴△OCE∽△ODB，∴S△OCES△ODB＝(OCOD)2，∵OC＝CD＝12OD，∴S△OCES△ODB＝(12)2＝14，设S△OCE＝a，则S△ODB

＝4a，∴S四边形BDCE＝3a，∴3a＝2，解得a＝23，∴S△OBD＝4a＝83，∵12|k|＝S△ODB，即12|k|＝83，解得k＝±163，∵反比例函数图象的一支在第二象限，∴k＜0，∴k＝－163.2.(1)证明：如解图，连接AE、OD，第2题解图∵∠ACB＝90°，∴AE

为⊙O的直径，∴O为AE的中点，又∵D为AB的中点，∴OD为△AEB的中位线，∴OD∥BE，∴∠ODF＝∠DFB，∵DF⊥BC，∴∠DFB＝90°，∴∠ODF＝90°，即OD⊥DF，又∵OD是⊙O的半径，∴DF为⊙O的切线；(2)解：∵∠ACB＝90°，AC＝3，BC＝9，

∴在Rt△ABC中，由勾股定理得AB＝AC2＋BC2＝32＋92＝310，∵D为AB的中点，∴BD＝12AB＝3102，∵AE为⊙O的直径，∴∠ADE＝90°，∴∠BDE＝∠BCA＝90°，又∵∠B＝∠B，

∴△BDE∽△BCA，∴BDBC＝DEAC，即31029＝DE3，解得DE＝102.3.D【解析】∵四边形ABCD是矩形，∴AB⊥BC，又∵OE⊥BC，∠ACB＝∠ECO，∴△ABC∽△EOC，ABOE＝BCOC，∴BC·OE＝AB·OC，即S△DC

O＝S△BCE＝6，∴|k|＝2S△DCO＝12，∵反比例函数图象在第二象限，∴k＜0，∴k＝－12.4.(1)证明：∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∴∠DCE＝90°，即∠BCD＝∠DCE，∴∠E＋∠CDE＝90°，∵BF⊥DE，∴∠E＋∠EBF＝90°，∴∠EBF

＝∠CDE，在△BCG和△DCE中，＝＝BCDDCEBCCDEBFCDE，∴△BCG≌△DCE(ASA)，∴BG＝DE；(2)解：∵G是CD的中点，∴CG＝GD，则AB＝BC＝CD＝2CG，在Rt△BCG中，BG＝BC2＋CG2＝5CG，∵∠DFG＝∠BCG＝90°，

∠DGF＝∠BGC，∴△DGF∽△BGC，∴GFCG＝GDGB，即GFCG＝CG5CG，∴GF＝55CG，∵AB∥CD，∴△GHC∽△BHA，∴GHBH＝CGAB，即GHBH＝CG2CG，∴HG＝12BH，∴HG＝13BG＝53CG，

∴HGGF＝53CG55CG＝53.5.证明：(1)∵OE＝OB，∴∠OBE＝∠OEB，∵四边形ABCD是平行四边形，∴OB＝OD，∴OE＝OD，∴∠ODE＝∠OED，∵在△BED中，∠OBE＋∠OEB＋

∠OED＋∠ODE＝180°，∴2∠OEB＋2∠OED＝180°，∴∠OEB＋∠OED＝90°，即∠BED＝90°，∴DE⊥BE；(2)如解图，设OE交CD于点H.第5题解图∵OE⊥CD，∴∠CHE＝90°，∴∠CEH＋∠DCE＝90°，

∵∠CED＝90°，∴∠CDE＋∠DCE＝90°，∴∠CDE＝∠CEH，∵∠OEB＝∠OBE，∴∠OBE＝∠CDE，又∵∠CED＝∠BED，∴△CED∽△DEB，∴CEDE＝CDDB，即BD·CE＝CD·DE.6.(1)证明：∵∠ABC＝9

0°，∴∠ABD＋∠DBC＝90°，∵CB＝CE，∴∠CBE＝∠E，∵DE是⊙C的直径，∴∠DBE＝90°，∴∠DBC＋∠CBE＝∠DBC＋∠ABD＝90°，∴∠ABD＝∠CBE＝∠E，又∵∠BAD＝∠EAB，∴△ABD∽△AEB；(2)解：令AB

＝4x，则BC＝3x，由勾股定理得AC＝5x，∵CD＝BC＝3x，∴AD＝2x，AE＝8x，由(1)知，△ABD∽△AEB，∴ABAE＝BDBE＝ADAB，∴BDBE＝2x4x＝12，∵∠DBE＝90°，∴tanE＝BDBE＝

12；(3)解：如解图，过点A作EB延长线的垂线，垂足为点G，第6题解图∵AF平分∠BAC，∴∠1＝∠2，又∵BC＝CE，∴∠3＝∠E，在△BAE中，有∠1＋∠2＋∠3＋∠E＝180°－90°＝90°，∴∠4＝∠2＋∠E＝45°，∴△GAF为等腰直角三角形，∵AF＝2

，∴AG＝2，由(2)可知，AE＝8x，tanE＝12，∴AG＝55AE＝855x，即855x＝2，解得x＝108，∴半径r＝3x＝3108.7.(1)证明：∵AB＝AC，BD＝CD，∴AD⊥BC，∵CE⊥AB，∴∠ADB＝∠CEB＝90°，又∵∠B＝∠

B，∴△ABD∽△CBE；(2)解：∵BD＝3，∴BC＝2BD＝6，∵△ABD∽△CBE，∴BDBE＝ABBC，即32＝AB6，解得AB＝9，∴AC＝AB＝9.8.(1)证明：∵⊙O与DE相切于点B，AB为⊙O的直径，∴∠ABE

＝90°，∴∠BAE＋∠E＝90°，又∵∠DAE＝90°，∴∠BAD＋∠BAE＝90°，∴∠BAD＝∠E；(2)解：如解图，连接BC，第8题解图∵AB为⊙O的直径，∴∠ACB＝90°，∵AC＝8，AB＝2×5＝10，∴BC＝AB2－AC2＝6，

∵∠BCA＝∠ABE＝90°，∠BAD＝∠E，∴△ABC∽△EAB，∴ACBE＝BCAB，即8BE＝610，∴BE＝403.9.证明：(1)∵AB＝AC，∴∠B＝∠C，∵∠B＋∠BED＋∠EDB＝180°，∠BED＋∠DEF＋∠FEC＝180°，∠DEF＝∠B，∴∠EDB＝∠FE

C，∵∠B＝∠C，∴△BDE∽△CEF；(2)由(1)知△BDE∽△CEF，∴BECF＝DEEF，∵BE＝CE，∴CECF＝DEEF，又∵∠B＝∠C＝∠DEF，∴△EDF∽△CEF，∴∠DFE＝∠EFC，∴FE平分∠DFC.10.(1)

证明：∵△ABC为等边三角形，∴∠B＝∠C＝60°，∴∠BED＋∠EDB＝180°－60°＝120°，∵∠EDF＝60°，∴∠EDB＋∠FDC＝180°－60°＝120°，∴∠BED＝∠FDC，∴△BDE∽△CFD；(2)解：由(1)知△BDE∽△CFD，∴BECD＝BDCF，∵BC＝6，

BD＝1，∴CD＝BC－BD＝5，∴BE5＝13，解得BE＝53.11.证明：∵四边形ABCD是正方形，∴∠B＝∠C＝90°，∴∠BEF＋∠EFB＝90°，∵∠EFG＝90°，∴∠EFB＋∠CFG＝1

80°－90°＝90°，∴∠BEF＝∠CFG，∴△EBF∽△FCG.12.解：如解图，分别过点A、B作AC⊥x轴于点C，BD⊥x轴于点D，第12题解图则∠ACO＝∠BDO＝90°，∴∠1＋∠2＝90°，又∵∠AOB＝9

0°，∴∠2＋∠3＝90°，∴∠1＝∠3，∴△BOD∽△OAC，∴ODAC＝BDOC＝BOOA，∵A(2，1)，∴OC＝2，AC＝1，OA＝5，又∵BO＝25，∴OD1＝BD2＝255，∴OD＝2，BD＝4，∴B(－

2，4)．把B(－2，4)代入y＝kx得k＝－8，∴反比例函数的解析式为y＝－8x.13.(1)证明：∵AB为半圆O的直径，∴∠ACB＝90°，∴∠BAC＋∠ABC＝90°，∵AE为半圆O的切线，∴∠BAE＝90°，∴∠EAD

＋∠BAC＝90°，∴∠EAD＝∠ABC，∵OD⊥AC，∴∠ADE＝∠ACB＝90°，∴△EAD∽△ABC，∴EAAB＝ADBC，∴AE·BC＝AD·AB；(2)解：如解图，设BF与半圆O交于点G，连接AG，则∠AGB＝∠ACB＝90°，第13题解图∵∠A

DG＝∠BDC，∴△ADG∽△BDC，∴AGBC＝DGDC，∵在Rt△ABC中，BC＝AB·sin∠BAC＝10×35＝6，∴AC＝AB2－BC2＝8，∵OD⊥AC，∴AD＝CD＝12AC＝4，∴AGDG＝BCCD＝64＝32，

设AG＝3x，则DG＝2x，由勾股定理得AG2＋DG2＝AD2，即9x2＋4x2＝42，解得x＝41313，则AG＝121313，∴BG＝AB2－AG2＝341313，∵∠AFG＋∠FAG＝90°，∠FAG＋∠GAB＝90°，∴∠AFG＝∠BAG，∴△AGF∽△

BGA，∴AGBG＝AFBA，即121313341313＝AF10，∴AF＝6017.