【文档说明】2021年人教版高中数学必修第二册课时同步检测6.3.2《平面向量的正交分解及坐标表示》（原卷版）.doc，共(3)页，206.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38923.html

以下为本文档部分文字说明：

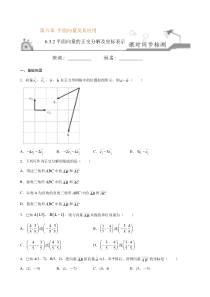
第六章平面向量及其应用6.3.2平面向量的正交分解及坐标表示一、基础巩固1．向量1e，2e，a，b在正方形网格中的位置如图所示，则ab（）A．1242eeB．1224eeC．123eeD．123ee2．下列可作为正交

分解的基底的是（）A．等边三角形ABC中的AB和ACB．锐角三角形ABC中的AB和ACC．以角A为直角的直角三角形ABC中的AB和ACD．钝角三角形ABC中的AB和AC3．已知13A，，41B，，则与向量AB共线的单位向量为（）A．435

5，或4355，B．3455，或3455，C．4355，或4355，D．3455，或3455，4．已知A(3，7)，B(5，2)，把向量AB按向量=(1，2)平移后，所得向量AB

的坐标是（）A．(2，－5)B．(1，－7)C．(0，4)D．(3，－3)5．已知ABCD为平行四边形，其中A(5，－1)，B(－1，7)，C(1，2)，则顶点D的坐标为（）A．(－7，0)B．(7，6)C．(

6，7)D．(7，－6)6．在平面直角坐标系xOy中，点3,1P，将向量OP绕点O按逆时针方向旋转2后得到向量OQ，则点Q的坐标是（）A．2,1B．1,2C．3,1D．1,37．已知线性相关的变量x，y，设其样本点为,iii

Axy（1,2,,6i），回归直线方程为2yxb，若1262,6OAOAOA（O为坐标原点），则b（）A．3B．53C．12D．128.22420210fxxxxx的最小值为()A．25B．52C．4D．

89．（多选）已知点4,6A，33,2B，与向量AB平行的向量的坐标可以是（）A．14,33B．97,2C．14,33D．(7，9)10．（多选）已知向量(1,0)i，(0,1)j，对平面内的任一向量

a，下列结论中错误的是（）A．存在唯一的一对实数x，y，使得(,)axyB．若1212,,,xxyyR，1122,,axyxy，则12xx，且12yyC．若,xyR，(,)axy，且0a，则a的起点是原点OD．若,xyR，0a，且a的终点坐标是

(,)xy，则(,)axy11．（多选）已知平行四边形的三个顶点的坐标分别是(3,7),(4,6),(1,2)ABC．则第四个顶点的坐标为（）A．(0,1)B．(6,15)C．(2,3)D．(2,3)12．（多选）已知ABC是边长为2的等边三角形，D，E分别是AC、AB上

的两点，且AEEB，2ADDCuuuruuur，BD与CE交于点O，则下列说法正确的是（）A．1ABCEB．0OEOCC．32OAOBOCD．ED在BC方向上的投影为76二、拓展提升13．已知e是直线l上的

一个单位向量，向量a与b都是直线l上的向量，分别在下列条件下写出a与b的坐标：（1）3ae，6be；（2）14ae，2be.14．已知12,ee是平面内两个相互垂直的单位向量，且122aee，1232bee，13c

e，求,,abc的坐标.15．已知向量(,2)ax，(2,4)b．（1）若//ab，求实数x的值；（2）若6ab，求实数x的值．