【文档说明】2021年人教版高中数学必修第二册(精讲)6.1《平面向量的概念》（解析版）.doc，共(12)页，832.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38793.html

以下为本文档部分文字说明：

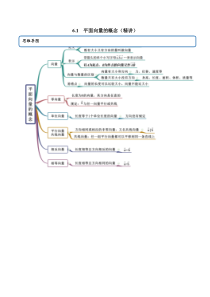
6.1平面向量的概念（精讲）思维导图考法一向量与数量的区别【例1】（2020·全国高一）下列各量中是向量的是（）A．时间B．速度C．面积D．长度【答案】B常见考法【解析】既有大小，又有方向的量叫做向量；时间、面积、长度只有大小没有方向，因此不是向量．而速度既有大小

，又有方向，因此速度是向量．故选：B．【一隅三反】1．（2020·全国高一课时练习）下列量不是向量的是（）A．力B．速度C．质量D．加速度【答案】C【解析】质量只有大小，没有方向，不是向量.故选C2．（2020·全国高一课时练习）给出下列物理量:①密度；②路程；③速度

；④质量；⑤功；⑥位移.下列说法正确的是()A．①②③是数量，④⑤⑥是向量B．②④⑥是数量，①③⑤是向量C．①④是数量，②③⑤⑥是向量D．①②④⑤是数量，③⑥是向量【答案】D【解析】【解析】由物理知识可知，密度，路程，质量，功只有大小，没有方向，因此是数量而速度

，位移既有大小又有方向，因此是向量.故选：D3．（2020·全国高一课时练习）下列说法正确的是（）A．数量可以比较大小，向量也可以比较大小B．方向不同的向量不能比较大小，但同向的可以比较大小C．向量的大小与方向有关D．向量的模可以比较大小【答案】D【解析】向量不能比较大小，向量的

模能比较大小，显然D正确.考法二向量的几何表示【例2】（2020·全国高一专题练习）某人从A点出发向东走了5米到达B点，然后改变方向沿东北方向走了102米到达C点，到达C点后又改变方向向西走了10米到达D点．（1）作出向量AB，BC，CD；（2）求AD的模．【答案】（1）见解析；（2）55A

D米【解析】（1）作出向量AB，BC，CD；如图所示：（2）由题意得，△BCD是直角三角形，其中∠BDC＝90°，BC＝102米，CD＝10米，所以BD＝10米．△ABD是直角三角形，其中∠ABD＝

90°，AB＝5米，BD＝10米，所以AD＝22510＝55(米)，所以|55AD米.【一隅三反】1.（2021·江苏高一）如图的方格由若干个边长为1的小正方形组成，方格中有定点A，点C为小正方形的顶点，且5AC，画出所有的向量AC.【答案】见解析【解析】∵||5AC

，∴C点落在以A为圆心，以5为半径的圆上，又∵点C为小正方形的顶点，根据该条件不难找出满足条件的点C，解析所有的向量AC，如图所示：2．（2020·全国高一课时练习）在如图所示的坐标纸（规定小方格的边长为1）中，用直尺和圆规画出下列向量：（1）||4OA,点A

在点O正南方向；（2）||22OB,点B在点O北偏西45方向；（3）||2OC,点C在点O南偏西30方向.【答案】（1）作图见解析（2）作图见解析（3）作图见解析【解析】如图.3．（2020·全国高一课时

练习）如图所示，某人从点A出发，向西走了200m后到达B点，然后改变方向，沿北偏西一定角度的某方向行走了10013m到达C点，最后又改变方向，向东走了200m到达D点，发现D点在B点的正北方.（1）作出向量AB，BC，CD（图中1个单位长度表示100m）；（2

）求向量DA的模.【答案】（1）作图见解析（2）10013m【解析】（1）如图，,,ABBCCD即为所求.（2）如图，作向量DA，由题意可知，四边形ABCD是平行四边形，∴||10013mDABC.考法三相等向量与共线向量【例3】（2020·全国）如图，四边形ABCD为正方形，△BCE

为等腰直角三角形.（1）图中与AB共线的向量有________；（2）图中与AB相等的向量有________；（3）图中与AB模相等的向量有_________________；（4）图中EC与BD是______向量（填“相等”

或“不相等”）；（5）AB与BA相等吗？【答案】（1）BE，CD，AE（2）BE（3）BC，CD，DA，BE（4）相等（5）不相等【解析】根据题意得，（1）图中与AB共线的向量为BE、DC、AE；（2）与AB相等的向量有BE；（3）图中与AB模相

等的向量有BC，CD，DA，BE；（4）相等；（5）AB与BA不相等；故答案为：（1）BE，CD，AE（2）BE（3）BC，CD，DA，BE（4）相等（5）不相等【一隅三反】1．（2020·全国高一课时练习）如图，ABC和ABC是在

各边的三等分点处相交的两个全等的等边三角形，设ABC的边长为a，图中列出了长度均为3a的若干个向量，则（1）与向量GH相等的向量有______；（2）与向量GH共线，且模相等的向量有______；（3）与向量EA共线，且模相等的向量有________.【答案】,LBH

C,,,,ECLELBGBHC,,,,EFFBHAHKKB【解析】（1）与向量GH相等的向量有,LBHC；（2）与向量GH共线，且模相等的向量有,,,,ECLELBGBHC；（3）与向量EA共线，且模相等的向量有,,,,EFFBHAHKKB.故答案为：,

LBHC；,,,,ECLELBGBHC；,,,,EFFBHAHKKB2．（2020·全国高一）在如图所示的向量,,,,abcderrrurr中（小正方形的边长为1），判断是否存在下列关系的向量：（1）是共线向量的

有______；（2）方向相反的向量有______；（3）模相等的向量有______.【答案】a和d，e和ba和d，b和e,,acdrrur【解析】（1）adrur∥，ebrr∥，故a和d，e和b是共线向量.（2）a和d，b和e是方向相反的向量.（3）由勾股定理可得

，模相等的向量有,,acdrrur.故答案为：（1）a和d，e和b；（2）a和d，b和e；（3）,,acdrrur.3．（2020·全国高一专题练习）如图所示，O是正六边形ABCDEF的中心，且OA＝a，OB＝b，OC＝c.（1）与a的长度相等、方向相反的向量有哪些？（2）与a共线的向量有

哪些？（3）请一一列出与a，b，c.相等的向量．【答案】（1）ODuuur，BC，AO，FE.（2）EF，BC，ODuuur，FE，CB，DO，AO，DA，AD.（3）与a相等的向量有EF，DO，CB；与b相等的向量有DC，EO，FA；与c相

等的向量有FO，ED，AB.【解析】（1）因为正六边形中各线段长度都相等，且方向相反的有：ODuuur，BC，AO，FE.（2）由共线向量定理得：EF，BC，ODuuur，FE，CB，DO，AO，DA，AD.与a共线.（3）由相等向量的定义得：与a相等的向量有EF，

DO，CB；与b相等的向量有DC，EO，FA；与c相等的向量有FO，ED，AB.考法四平面向量概念的区分【例4】（2020·天津静海区·高一学业考试）下列关于向量的结论：（1）任一向量与它的相反向量不相等；（2）向量a与b平行，则a与

b的方向相同或相反；（3）起点不同，但方向相同且模相等的向量是相等向量；（4）若向量a与b同向，且||||ab，则ab.其中正确的序号为（）A．（1）（2）B．（2）（3）C．（4）D．（3）【答案】D【解析】零向量与它的相反向量相等，故（1）错误；当向量a为零向量时，其方向是任

意的，不能说a与b的方向相同或相反，故（2）错误；相等向量是方向相同且模相等的向量，故（3）正确；向量是既有大小又有方向的量，向量只能相等，不能比较大小，故（4）错误.故选：D.【一隅三反】1．（2020·全国高一课时练习）下列命题中，正确的个数是（

）①单位向量都相等；②模相等的两个平行向量是相等向量；③若a，b满足ab且a与b同向，则ab；④若两个向量相等，则它们的起点和终点分别重合；⑤若a∥,bb∥c，则b∥c．A．0个

B．1个C．2个D．3个【答案】A【解析】解：对于①，单位向量的模长相等，但方向不一定相同，故①错误；对于②，模相等的两个平行向量是相等向量或相反向量，故②错误；对于③，向量是有方向的量，不能比较大小，故③错误；对于④，向量是可以自由平移的矢量，当两个向量相等时，它们的起点和终点不一定相同，故

④错误；对于⑤，0b时，若abbc∥，∥，则a与c不一定平行．综上，以上正确的命题个数是0．故选：A．2．（2020·安徽六安市·六安一中高一期末）下列说法不正确的是（）A．平行向量也叫共线向量B．两非零向量平行，则它们所在的直线平行或重合C．若a为非零向量

，则aa是一个与a同向的单位向量D．两个有共同起点且模相等的向量，其终点必相同【答案】D【解析】由于任一组平行向量都可以平移到一条直线上，则平行向量也叫共线向量，A正确；两非零向量平行，则它们所在的直线平行或重合，由共线向量的定义可知，B正确；aa的模长为1，10a，则aa是一个与a

同向的单位向量，C正确；从同一点出发的两个相反向量，有共同的起点且模长相等，但终点不同，D错误；故选：D2．（2021·甘肃兰州市）下列命题中正确的个数为（）①两个有共同始点且相等的向量，其终点可能不同；②若非零向量AB与CD共线，则A、B、C、D四点共线；③若非零向量a与b共线，则ab；

④四边形ABCD是平行四边形，则必有ABCD；⑤//ab，则a、b方向相同或相反.A．0个B．1个C．2个D．3个【答案】B【解析】①相等向量是大小相等、方向相同的向量，如果两个相等向量起点相同，则由定义知终点必相同，命题①是假命题；②共线向量是基线平行或重合的向量，若

非零向量AB与CD共线且直线AB与CD平行时，A、B、C、D四点不共线，命题②是假命题；③若非零向量a与b共线，则存在非零实数，使得ba，命题③是假命题；④四边形ABCD是平行四边形，则ABDC，由相等向量的定义可知ABDC，命题④是

真命题；⑤若a为非零向量，0b，则a、b方向无法确定，命题⑤是假命题.故选：B.