【文档说明】2021年人教版高中数学选择性必修第二册（精讲)拓展四《导数与零点、不等式的综合运用》（原卷版）.doc，共(5)页，265.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-38127.html

以下为本文档部分文字说明：

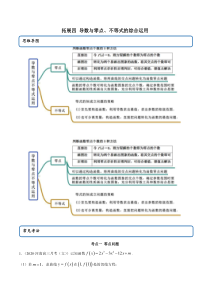
拓展四导数与零点、不等式的综合运用考点一零点问题1．（2020·河南高三月考（文））已知函数322312fxxxxm.（1）若1m，求曲线yfx在1,1f处的切线方程；思维导图常见考法（2）若函数fx有3个零点，求实数m的取值范围.【一

隅三反】1．（2020·山西运城·）已知函数ln21fxxaxaR.（1）讨论fx的单调性；（2）若fx有两个零点，求a的取值范围.2．（2020·陕西安康·高三三模（理））已知函数()ln()(0)x

afxexaa.（1）证明：函数()fx在(0,)上存在唯一的零点；（2）若函数()fx在区间(0,)上的最小值为1，求a的值.3．（2020·甘肃武威）设函()()1fxxanxxa，aR．（1）设()()gxfx，

求函数()gx的极值；（2）若1ea…，试研究函数()()1fxxanxxa的零点个数．考点二导数与不等式【例2】．（2021·湖南湘潭·月考（理））已知函数ln1()xxfxe．（1）求()fx的最大值；（2）当1x时，2(ln1)xaxxe恒成立，

求a的取值范围．【一隅三反】1．（2019·广东湛江·高二期末（文））已知函数()(1)ln()afxxaxaRx．（1）当01a时，求函数()fx的单调区间；（2）是否存在实数a，使()fxx恒成立，若

存在，求出实数a的取值范围；若不存在，说明理由．2．（2020·黑龙江萨尔图·大庆实验中学高二期末（文））已知函数()ln(0)fxxxx.（1）求()fx的单调区间和极值；（2）若对任意23(0,),()2xmxxfx恒成立

，求实数m的最大值.不等式恒成立求解参数范围的方法：（1）分离参数并构造函数解决问题；（2）采用分类讨论的方式解决问题.3．（2020·安徽省含山中学月考（理））已知函数211()ln(,0)22fxx

axaRa.（1）当2a时，求曲线()yfx在点(1,(1))f处的切线方程；（2）求函数()fx的单调区间；（3）若对任意的[1,)x，都有()0fx成立，求a的取值范围.