【文档说明】2021年人教版高中数学选择性必修第三册7.4《二项分布与超几何分布》同步精讲（解析版）.doc，共(14)页，774.500 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-37484.html

以下为本文档部分文字说明：

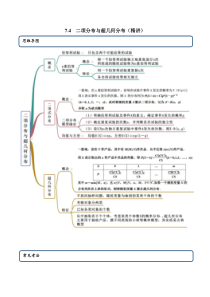
7.4二项分布与超几何分布（精讲）思维导图常见考法考法一二项分布【例1】（2020·全国高二课时练习）高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行､水平间隔相等的圆柱形铁钉(如图)，并且每一排铁钉数目都比上一排多一个，一排中各个铁钉恰好对准上

面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗铁钉间隔的小球，当小球从两钉之间的间隙下落时，由于碰到下一排铁钉，它将以相等的可能性向左或向右落下，接着小球再通过两铁钉的间隙，又碰到下一排铁钉.如此继续下去，在最底层的5个出口处各放置一个容器接住小球.（1

）理论上，小球落入4号容器的概率是多少？（2）一数学兴趣小组取3个小球进行试验，设其中落入4号容器的小球的个数为X，求X的分布列.【答案】（1）14；（2）分布列答案见解析.【解析】（1）记“小球落入4号容器”为事件A，若要小球落入4号容器，则

需要在通过的四层中有三层向右，一层向左，∴理论上，小球落入4号容器的概率43411()C24PA.（2）落入4号容器的小球的个数X的所有可能取值为0，1，2，3，303127(0)C1464PX

，2131127(1)C14464PX，2123119(2)C14464PX，33311(3)C464PX，

X的分布列为X0123P27642764964164【一隅三反】1．（2020·重庆市第七中学校高二月考）若随机变量14,2XB～，则21EX（）A．2B．3C．4D．5【答案】D【解析】因为14,2XB～，所以142

2EX，所以21215EXEX.故选：D.2．（多选）（2020·全国高二单元测试）已知随机变量120,3XB，若使()PXk的值最大，则k等于（）A．5B．6C．7D．8【答案】BC【解析】令120112020201212033

1221233kkkkkkCPXkkPXkkC，得k6，即当k6时，()1()PXkPXk；当6k时，()()76PXPX；当6k时，()1

()PXkPXk，所以(6)PX和()7PX的值最大.故选：BC.3．（2020·江苏淮安市·淮阴中学高二期末）江苏实行的“新高考方案：312”模式，其中统考科目：“3”指语文、数学、外语三门，不分文理：学生根据高校的要求，结合

自身特长兴趣，“1”指首先在在物理、历史2门科目中选择一门；“2”指再从思想政治、地理、化学、生物4门科目中选择2门某校，根据统计选物理的学生占整个学生的34；并且在选物理的条件下，选择地理的概率为23；在选历史的条件下，选地理的概率为45．（1）求该校最终选地理的学生概率；（2）该校甲、乙、丙

三人选地理的人数设为随机变量X．①求随机变量2X的概率；②求X的概率分布列以及数学期望．【答案】（1）710；（2）①4411000；②分布列见解析，2110EX.【解析】（1）该校最终选地理的学生为事件A，32147434510PA；因此，该校最终选地理的学生为

710；（2）①由题意可知，73,10XB，所以，22373441210101000PXC；②由于73,10XB，则33270101000PX，121373189110101

000PXC，22373441210101000PXC，33373433101000PXC，所以，随机变量X的分布列如下表所示：X0123P27100018910004

411000343100072131010EX．4．（2020·陕西渭南市）已知某植物种子每粒成功发芽的概率都为13，某植物研究所分三个小组分别独立进行该种子的发芽试验，每次试验种一粒种子，每次试验结

果相互独立.假设某次试验种子发芽，则称该次试验是成功的，如果种子没有发芽，则称该次试验是失败的.（1）第一小组做了四次试验，求该小组恰有两次失败的概率；（2）第二小组做了四次试验，设试验成功与失败的次数的差的绝对值为X，求X的分布列及数学期望.【答案】（1）827；（

2）答案见解析；14881.【解析】（1）记“该小组有两次失败”为事件A，222412248()338127PAC.（2）由题意可知X的可能取值为0，2，4.2224128(0)3327PXC

，13311344121232840(2)33338181PXCC，4404442116117(4)338181PXCC.故X的分布列为：X024P82740811781840

17148()02427818181EX.考点二超几何分布【例2】（2020·全国高二单元测试）现对某高校16名篮球运动员在多次训练比赛中的得分进行统计，将每位运动员的平均成绩所得数据用频率分布直方图表示如下．(如：落在区间[10，15)内的频率/组距为0.01

25)规定分数在[10，20)，[20，30)，[30，40)上的运动员分别为三级篮球运动员、二级篮球运动员、一级篮球运动员，现从这批篮球运动员中利用分层抽样的方法选出16名运动员作为该高校的篮球运动员代表．（1）求a的值和选出篮球运动员代表中一级运动员的人数；（2）若从篮球运动员代表中选出

三人，求其中含有一级运动员人数X的分布列；（3）若从该校篮球运动员中有放回地选三人，求其中含有一级运动员人数Y的期望．【答案】（1）a＝0.0250，4人；（2）答案见解析；（3）34.【解析】（1）由频率分布直方图知：(0.0625＋0.0500＋0.

0375＋a＋2×0.0125)×5＝1，∴a＝0.0250.其中为一级运动员的概率为(0.0125＋0.0375)×5＝0.25，∴选出篮球运动员代表中一级运动员为0.25×16＝4人．（2）由已知可得X的可能取值分别为0，1，2，3

，P(X＝0)＝312316CC＝1128，P(X＝1)＝21243161CCC＝3370，P(X＝2)＝24113162CCC＝970，P(X＝3)＝34316CC＝1140，∴X的分布列为X0123P112833709701

140（3）由已知得Y～B1(3,)4，∴E(Y)＝np＝3×14＝34，∴含有一级运动员人数Y的期望为34.【一隅三反】1．（2020·全国高二课时练习）新冠肺炎疫情期间，为了更有效地进行防控，各地学校都发

出延期开学的通知.很多学校及老师为响应各地教育行政部门实行“停课不停学”的号召，让学生们在家通过收看网络直播的方式进行学习，已知高一某班共有学生21人，其中男生12人，女生9人.现采用分层抽样的方法从中抽取7人，测试他们对网络课程学习的效果，效果分为优秀和不优秀两种

，优秀得2分，不优秀得1分.（1）应抽取男生､女生各多少人？（2）若抽取的7人中，4人的测试效果为优秀，3人为不优秀，现从这7人中随机抽取3人.（i）用X表示抽取的3人的得分之和，求随机变量x的分布列及数学期望；（ii）设事件A为“抽取的3人中，既有测试

效果为优秀的，也有为不优秀的”，求事件A发生的概率.【答案】（1）4人；（2）（i）分布列答案见解析，数学期望：337；（ii）67.【解析】（1）因为采用分层抽样的方法进行抽样，所以应抽取女生97321人，抽取男生127421人.（2）（i）随机变量X的所有可能取值为3，4，

5，6.0343371(3)35CCPXC，12433712(4)35CCPXC，21433718(5)35CCPXC，3043374(6)35CCPXC，所以随机变量X的分布列为X3456P13512351835435数

学期望11218416533()345635353535357EX.（ii）由（i）知12186()(4)(5)35357PAPXPX，故事件A发生的概率为67.2．（2020·绵阳市·四川省绵阳江油中学）某校五四青年艺术节

选拔主持人，现有来自高一年级参赛选手4名，其中男生2名;高二年级参赛选手4名，其中男生3名.从这8名参赛选手中随机选择4人组成搭档参赛.（Ⅰ）设A为事件“选出的4人中恰有2名男生，且这2名男生来自同一个年级”，求事件A发生的概率;（Ⅱ）设X为选出的

4人中男生的人数，求随机变量X的分布列和数学期望.【答案】（Ⅰ）635（Ⅱ）分布列见解析，数学期望52【解析】（Ⅰ）由已知有2222233348635CCCCPAC，所以事件A发生的概率为635

.（Ⅱ）随机变量X的所有可能取值为1，2，3，4，453481,2,3,4kkCCPXkkC所以随机变量X的分布列为X1234P1143737114所以随机变量X的数学期望1331512341477142EX.3．（2021·北京东城区）

为了解学生自主学习期间完成数学套卷的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表.（1）从这班学生中任选一名男生，一名女生，求这两名学生完成套卷数之和为4的概率？（2）若从完成套卷数不少于4套的学生中任选4人，设选到的男学生人数为X，求随机变量X的分布列和数学期望

；（3）试判断男学生完成套卷数的方差21s与女学生完成套卷数的方差22s的大小（只需写出结论）.【答案】（1）796（2）详见解析（3）2212ss【解析】（1）设事件A：从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数

之和为4,由题意可知,1341712896PA.（2）完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故X的取值为0,1,2,3,4.由题意可得44481070CPXC；13444816817035CCPXC

；224448361827035CCPXC；31444816837035CCPXC；44481470CPXC.所以随机变量X的分布列为X01234P1708351835835170随机变量X的均值116361610

123427070707070EX.(3)2212ss.考点三二项分布与超几何分布综合运用【例3】（2020·浙江台州市·高二期中）2020年五一期间，银泰百货举办了一次有奖促销活动，消费每超过600元(含600元)，均可

抽奖一次，抽奖方案有两种，顾客只能选择其中的一种.方案一：从装有10个形状､大小完全相同的小球(其中红球2个，白球1个，黑球7个)的抽奖盒中，一次性摸出3个球其中奖规则为：若摸到2个红球和1个白球，享受免单优惠；若摸出2个红球和1个黑

球则打5折；若摸出1个白球2个黑球，则打7折；其余情况不打折.方案二：从装有10个形状､大小完全相同的小球(其中红球3个，黑球7个)的抽奖盒中，有放回每次摸取1球，连摸3次，每摸到1次红球，立减200元.（1）若两个顾客均分别消费了60

0元，且均选择抽奖方案一，试求两位顾客均享受免单优惠的概率；（2）若某顾客消费恰好满1000元，试从概率角度比较该顾客选择哪一种抽奖方案更合算？【答案】（1）114400；（2）选择第二种方案更合算.【解析】（1）选择方案一若享受到免单优惠，则需

要摸出三个红球，设顾客享受到免单优惠为事件A，则21213101120CCPAC，所以两位顾客均享受到免单的概率为114400PPAPA；（2）若选择方案一，设付款金额为X元，则X可能的取值为0、500、700、1000.212131010

120CCPXC，21273107500120CCPXC，1217310770040CCPXC，177911000112012040120PX.故X的分布列为，X05007

001000P1120712074091120所以177910500700100091012012040120EX（元）.若选择方案二，设摸到红球的个数为Y，付款金额为Z，则1000200ZY，由已知可得3~3,10YB，故

3931010EY，所以10002001000200820EZEYEY（元）.因为EXEZ，所以该顾客选择第二种抽奖方案更合算.【一隅三反】1．（2020·辽宁大连市）学校游园活动有这样一个游戏项目：甲箱子里

装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（1）求在1次游戏中，①摸出3个白球的概率；②获奖的概率；（

2）求在4次游戏中获奖次数X的分布列及数学期望()EX.【答案】（1）①15，②710；（2）分布列见解析，145.【解析】（1）设“在1次游戏中摸出i个白球”为事件(0,1,2,3),iAi①2132322531().5CCPACC

·②设“在1次游戏中获奖”为事件B，则23BAA，又21121332222222253531(),2CCCCCPACCCC··且A2，A3互斥，所以23117()()().2510PBPAPA=+=+=（2）由题意可知X的所有可能取值为0，1，2，3，4

，由（1）7()10PB，3()1()10PBPB，44381(0)()1010000PXPB，331473189(1)()()410102500PXCPBPB，222224731323(2)()()6101050

00PXCPBPB3334731029(3)()()410102500PXCPBPB4472401(4)()1010000PXPB所

以X的分布列是X01234P811000018925001323500010292500240110000显然7~B410X，，所以X的数学期望E(X)=7144105．2．（2020·广东云浮市）甲、乙去某公司应聘面试.该

公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题，按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成，2道题不能完成；应聘者乙每题正确完成的概率都是23，且每题正确完成与否互不影响.(1)分别求甲

、乙两人正确完成面试题数的分布列，并计算其数学期望;(2)请分析比较甲、乙两人谁的面试通过的可能性较大?【答案】(1)甲、乙的分布列见解析；甲的数学期望2、乙的数学期望2；(2)甲通过面试的概率较大．【解析】（1

）设X为甲正确完成面试题的数量，Y为乙正确完成面试题的数量，依题意可得：~(6,3,4)XH，∴1223461(1)5CCPXC，4212363(2)5CCPXC，3042361(3)5CCPXC，∴X的分布列为：X1

23P153515∴1311232555EX．2~3,3YB，∴0303211(0)3327PYC，12132162(1)C33279PY

，212321124(2)C33279PY，3033218(3)3327PYC，∴Y的分布列为：Y0123P1272949827∴124801232279927EY

．（2）2221312(12)(22)(32)5555DX，2121333(3)DYnpp，∵DXDY，∴甲发挥的稳定性更强，则甲通过面试的概率较大．3．（2021·哈尔滨市）一批产品共10件，其中3件是不合格

品，用下列两种不同方式从中随机抽取2件产品检验：方法一：一次性随机抽取2件；方法二：先随机抽取1件，放回后再随机抽取1件.记方法一抽取的不合格产品数为1.记方法二抽取的不合格产品数为2.（1）求两种抽取方式下1，2的概率分布列；（2）比较两种抽取方式抽到的不

合格品平均数的大小？并说明理由.【答案】（1）1，2的分布列见解析；（2）平均数相等，理由见解析.【解析】（1）方法一中随机变量1可取的值为0，1，2，且1服从超几何分布，于是023712107015CCPC；

113712107115CCPC；203712101215CCPC；因此1的频率分布可表示为下表：1012P715715115方法二中随机变量2可取的值为0，1，2，且2服从二项分布

，于是02022374901010100PC；12237211101050PC；202223721010PC；因此2的频率分布可表示为

下表：2012P4910021509100（2）由（1）知，方法一中1的数学期望为177130121515155E，方法二中2的数学期望为2332105E，所以两种方式抽

到的不合格品平均数相等.