【文档说明】(通用版)中考数学总复习第25课时《尺规作图》课时练习（教师版）.doc，共(5)页，116.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-35358.html

以下为本文档部分文字说明：

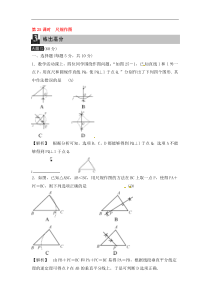
第25课时尺规作图(60分)一、选择题(每题5分，共10分)1．数学活动课上，四位同学围绕作图问题：“如图25－1，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q.”分别作出了下列四个图形．其中作法错误的是(A)【解析】根据分析可知，选项B，C，D都能够得到PQ⊥l于

点Q；选项A不能够得到PQ⊥l于点Q.2．如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA＋PC＝BC，则下列选项正确的是(D)【解析】由PB＋PC＝BC和PA＋PC＝BC易得PA＝P

B，根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上，于是可判断D选项正确．二、填空题(每题5分，共5分)3．用直尺和圆规作△ABC，使BC＝a，AC＝b，∠B＝35°，若这样的三角形只能作一个，则a，b间满足

的关系式是__sin35°＝ba或b≥a__.【解析】如答图所示：若这样的三角形只能作一个，则a，b间满足的关系式是：①当AC⊥AB时，即sin35°＝ba；②当b≥a时．三、解答题(共40分)4．(10分)如图，将线段AB放在边长为1的小正方形网格中，点A，点B均落在格点上，请用无刻

度直尺在线段AB上画出点P，使AP＝2173，并保留作图痕迹．(备注：本题只是找点不是证明，只需连结一对角线就行)解：由勾股定理得，AB＝42＋12＝17，所以AP＝2173时，AP∶BP＝2∶1.点P如答图所示．5．(15分)

如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于12GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E.(1)求证：

AB＝AE；(2)若∠A＝100°，求∠EBC的度数．解：(1)证明：∵AD∥BC，∴∠AEB＝∠EBC.由BE是∠ABC的角平分线，得∠EBC＝∠ABE，∴∠AEB＝∠ABE，∴AB＝AE；(2)由∠A＝100°，∠ABE＝∠AEB，得∠ABE＝∠AEB＝40°.由(1)得∠

EBC＝∠AEB＝40°.6．(15分)如图，已知锐角△ABC.(1)过点A作BC边的垂线MN，交BC于点D(用尺规作图法，保留作图痕迹，不要求写作法)；(2)在(1)的条件下，若BC＝5，AD＝4，tan∠BAD＝34，求DC的长．解：(1)如答图，直线MN即为所求；(2)∵AD⊥BC，∴∠AD

B＝∠ADC＝90°，在Rt△ABD中，∵tan∠BAD＝BDAD＝34，∴BD＝34×4＝3，∴DC＝BC－BD＝5－3＝2.(30分)7．(15分)如图，在平行四边形ABCD中，AB＜BC.(1)利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等(不写作法，保留作图痕迹

)；(2)若BC＝8，CD＝5，求CE.解：(1)如答图所示，E点即为所求；(2)∵四边形ABCD是平行四边形，∴AB＝CD＝5，AD∥BC，∴∠DAE＝∠AEB，∵AE是∠BAD的平分线，∴∠DAE＝∠BA

E，∴∠BAE＝∠BEA，∴BE＝BA＝5，∴CE＝BC－BE＝3.8．(15分)如图，已知在△ABC中，∠A＝90°(1)请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切(保留作图痕迹，不写作法和证明)；(2)若∠B＝60°，AB＝

3，求⊙P的面积．解：(1)如答图所示，则⊙P为所求作的圆；(2)∵∠B＝60°，BP平分∠ABC，∴∠ABP＝30°，∵tan∠ABP＝APAB，∴AP＝3，∴S⊙P＝3π.9．(15分)如图，△ABC是直角三角形，∠ACB＝90°.(1)尺规作图：作⊙

C，使它与AB相切于点D，与AC相交于点E，保留作图痕迹，不写作法，请标明字母；(2)在你按(1)中要求所作的图中，若BC＝3，∠A＝30°，求劣弧DE的长．解：(1)如答图，⊙C即为所求；(2)∵⊙C

切AB于D，∴CD⊥AB，∴∠ADC＝90°，∴∠DCE＝90°－∠A＝90°－30°＝60°，∴∠BCD＝90°－∠ACD＝30°，在Rt△BCD中，∵cos∠BCD＝CDBC，∴CD＝3cos30°＝332，∴劣弧DE的长为60·π·332180＝32π.