【文档说明】高考数学(文数)一轮复习课件 第五章 数列 第四节 数列求和(含详解).ppt，共(32)页，469.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-33633.html

以下为本文档部分文字说明：

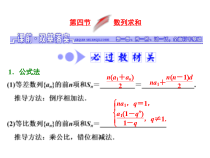
第四节数列求和na1＋an2na1＋nn－1d2na1，q＝1，a11－qn1－q，q≠1.1．公式法nn＋12n(n＋1)n22．几种数列求和的常用方法(2)裂项相消法：把数列的通项拆成两项之差，在求和时中间的

一些项可以相互抵消，从而求得前n项和．常用的裂项公式有：①1nn＋1＝____________；②12n－12n＋1＝__________________；③1n＋n＋1＝______________.1

n－1n＋11212n－1－12n＋1n＋1－n(3)错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么求这个数列的前n项和即可用错位相减法求解．(4)倒序相加法：如果一个数列{an}与首末两端等“距

离”的两项的和相等或等于同一个常数，那么求这个数列的前n项和即可用倒序相加法求解．1．若Sn＝1－2＋3－4＋5－6＋„＋(－1)n－1·n，则S50＝_____．答案：－25[小题体验]2．(教材习题改编)数列112，314，518，7116，„，(2n－1)＋12n，„的前

n项和Sn的值等于________．答案：n2＋1－12n1．直接应用公式求和时，要注意公式的应用范围，如当等比数列公比为参数(字母)时，应对其公比是否为1进行讨论．2．在应用错位相减法时，注意观察未合并项的正负号；结论中形如an，an＋1的式子应进行合并．3．在应用裂项相消法时，要

注意消项的规律具有对称性，即前剩多少项则后剩多少项．1．设f(n)＝2＋24＋27＋210＋„＋23n＋10(n∈N*)，则f(3)＝________．[小题纠偏]答案：27(87－1)2．已知数列{an}的前n项

和为Sn且an＝n·2n，则Sn＝________．答案：(n－1)2n＋1＋2考点一公式法求和[题组练透]1．(2017·重庆适应性测试)在数列{an}中，an＋1－an＝2，a2＝5，则数列{an}的前4项和为()A．9B．22C．24D

．32解析：依题意得，数列{an}是公差为2的等差数列，a1＝a2－2＝3，因此数列{an}的前4项和等于4×3＋4×32×2＝24，选C．答案：C2．若等比数列{an}满足a1＋a4＝10，a2＋a5＝

20，则{an}的前n项和Sn＝________．解析：由题意a2＋a5＝q(a1＋a4)，得20＝q×10，故q＝2，代入a1＋a4＝a1＋a1q3＝10，得9a1＝10，即a1＝109．故Sn＝1091－2n1－2＝109(2n－1)．答案：109(2n－1)3．已知等差

数列{an}满足a3＝2，前3项和S3＝92．(1)求{an}的通项公式；(2)设等比数列{bn}满足b1＝a1，b4＝a15，求{bn}的前n项和Tn．解：(1)设{an}的公差为d，则由已知条件得

a1＋2d＝2，3a1＋3×22d＝92，化简得a1＋2d＝2，a1＋d＝32，解得a1＝1，d＝12，故{an}的通项公式an＝1＋n－12，即an＝n＋12．(2)由(1)得b1＝1，b4＝a15＝15＋12

＝8．设{bn}的公比为q，则q3＝b4b1＝8，从而q＝2，故{bn}的前n项和Tn＝b11－qn1－q＝1×1－2n1－2＝2n－1．[谨记通法]数列求和应从通项入手，若无通项，则先求通项，然后通过对通项变形，转化为等差或等比或可求数列

前n项和的数列来求之．考点二分组转化法求和解：(1)设等比数列{bn}的公比为q，则q＝b3b2＝93＝3，所以b1＝b2q＝1，b4＝b3q＝27，所以bn＝3n－1(n∈N*)．设等差数列{an}的公

差为d．因为a1＝b1＝1，a14＝b4＝27，所以1＋13d＝27，即d＝2．所以an＝2n－1(n∈N*)．[典例引领](2016·北京高考)已知{an}是等差数列，{bn}是等比数列，且b2＝3，b3＝9，a1＝b1，a14＝b4．(1)求{an}的通项公式；(2)设cn＝an＋

bn，求数列{cn}的前n项和．(2)由(1)知，cn＝an＋bn＝2n－1＋3n－1．从而数列{cn}的前n项和Sn＝1＋3＋„＋(2n－1)＋1＋3＋„＋3n－1＝n1＋2n－12＋1－3n1－3＝n2＋3n－12．[由题悟法]分组转化法

求和的常见类型[提醒]某些数列的求和是将数列转化为若干个可求和的新数列的和或差，从而求得原数列的和，注意在含有字母的数列中对字母的讨论．[即时应用](2017·兰州实战考试)在等差数列{an}中，a2＋a7＝－23，a3＋a8＝－29．(1)求数列{an}的通项

公式；(2)设数列{an＋bn}是首项为1，公比为q的等比数列，求{bn}的前n项和Sn．解：(1)设等差数列{an}的公差是d．∵a3＋a8－(a2＋a7)＝2d＝－6，∴d＝－3，∴a2＋a7＝2a1＋7d＝－23，解得a1＝－1，∴数列{an}的通项公式为an＝－

3n＋2．(2)∵数列{an＋bn}是首项为1，公比为q的等比数列，∴an＋bn＝qn－1，即－3n＋2＋bn＝qn－1，∴bn＝3n－2＋qn－1．∴Sn＝[1＋4＋7＋…＋(3n－2)]＋(1＋q＋q2＋„＋qn－1)＝n3n－12＋(1＋q＋q2＋„＋qn－1)，故当q＝1时，Sn＝

n3n－12＋n＝3n2＋n2；当q≠1时，Sn＝n3n－12＋1－qn1－q．考点三错位相减法求和[典例引领](2016·山东高考)已知数列{an}的前n项和Sn＝3n2＋8n，{bn}是等差数列，且an＝bn＋bn＋1．(1)求数列{bn}的通项公式；(2)令cn＝an＋

1n＋1bn＋2n，求数列{cn}的前n项和Tn．解：(1)由题意知，当n≥2时，an＝Sn－Sn－1＝6n＋5，当n＝1时，a1＝S1＝11，满足上式，所以an＝6n＋5．设数列{bn}的公差为d．由a

1＝b1＋b2，a2＝b2＋b3，即11＝2b1＋d，17＝2b1＋3d，可解得b1＝4，d＝3.所以bn＝3n＋1．(2)由(1)知cn＝6n＋6n＋13n＋3n＝3(n＋1)·2n＋1，又Tn＝c1＋c2＋„＋cn，得Tn＝3×[2×22＋

3×23＋…＋(n＋1)×2n＋1]，2Tn＝3×[2×23＋3×24＋…＋(n＋1)×2n＋2]，两式作差，得－Tn＝3×[2×22＋23＋24＋…＋2n＋1－(n＋1)×2n＋2]＝3×4＋41－2n1－2－n＋1×2

n＋2＝－3n·2n＋2，所以Tn＝3n·2n＋2．[由题悟法]用错位相减法求和的3个注意事项(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以

便下一步准确写出“Sn－qSn”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解．[即时应用](2017·泉州调研)已知等差数列{an}的前n项和Sn满足S3＝6，S5＝15．(1)求{an}的通项公式；(2

)设bn＝an2an，求数列{bn}的前n项和Tn．解：(1)设等差数列{an}的公差为d，首项为a1，∵S3＝6，S5＝15，∴3a1＋12×3×3－1d＝6，5a1＋12×5×5－1d＝1

5，(2)由(1)得bn＝an2an＝n2n，∴Tn＝12＋222＋323＋„＋n－12n－1＋n2n，①∴12Tn＝122＋223＋324＋„＋n－12n＋n2n＋1，②①－②得12Tn＝12＋122＋123＋„＋12n－n2n＋1＝

121－12n1－12－n2n＋1＝1－12n－n2n＋1，∴Tn＝2－2＋n2n．考点四裂项相消法求和裂项相消法求和是历年高考的重点，命题角度凸显灵活多变，在解题中要善于利用裂项相消的基本思想，变

换数列an的通项公式，达到求解目的．常见的命题角度有：(1)形如an＝1nn＋k型；(2)形如an＝1n＋k＋n型；(3)形如an＝n＋1n2n＋22型．[锁定考向]角度一：形如an＝1nn＋k型1．(2017·西安质检)等差数

列{an}的各项均为正数，a1＝1，前n项和为Sn；数列{bn}为等比数列，b1＝1，且b2S2＝6，b2＋S3＝8．(1)求数列{an}与{bn}的通项公式；(2)求1S1＋1S2＋„＋1Sn．解：(1)设等差数列{an}的公差为d，d＞0，{

bn}的公比为q，则an＝1＋(n－1)d，bn＝qn－1．依题意有q2＋d＝6，q＋3＋3d＝8，解得d＝1，q＝2或d＝－43，q＝9(舍去)．故an＝n，bn＝2n－1．(2)由(1)知Sn＝1＋2＋„＋n＝12n(n＋1)，1Sn＝

2nn＋1＝21n－1n＋1，∴1S1＋1S2＋„＋1Sn＝21－12＋12－13＋„＋1n－1n＋1＝21－1n＋1＝2nn＋1．角度二：

形如an＝1n＋k＋n型2．(2017·江南十校联考)已知函数f(x)＝xα的图象过点(4,2)，令an＝1fn＋1＋fn，n∈N*．记数列{an}的前n项和为Sn，则S2017＝()A．2016－1B．2017－1C．2018－1D．2018＋1解

析：由f(4)＝2可得4α＝2，解得α＝12，则f(x)＝x12．∴an＝1fn＋1＋fn＝1n＋1＋n＝n＋1－n，S2017＝a1＋a2＋a3＋„＋a2017＝(2－1)＋(3－2)＋(4－3)＋„＋(2017－2016)＋(2018－2017)＝

2018－1．答案：C角度三：形如an＝n＋1n2n＋22型3．正项数列{an}的前n项和Sn满足：S2n－(n2＋n－1)Sn－(n2＋n)＝0．(1)求数列{an}的通项公式an；(2)令bn＝n＋1n＋22a2n，数列{bn}的前n项和为Tn．证明：

对于任意的n∈N*，都有Tn<564．解：(1)由S2n－(n2＋n－1)Sn－(n2＋n)＝0，得[Sn－(n2＋n)](Sn＋1)＝0．由于{an}是正项数列，所以Sn>0，Sn＝n2＋n．于是a1＝S1＝2，当n≥2时，an＝Sn－Sn－1＝n2＋n－(n－

1)2－(n－1)＝2n．综上，数列{an}的通项公式为an＝2n．(2)证明：由于an＝2n，故bn＝n＋1n＋22a2n＝n＋14n2n＋22＝1161n2－1n＋22．Tn＝1161－132＋122－142＋132－152＋„

＋1n－12－1n＋12＋1n2－1n＋22＝1161＋122－1n＋12－1n＋22<1161＋122＝564．[通法在握]利用裂项相消法求和的注意事项(1)抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项；(2

)将通项裂项后，有时需要调整前面的系数，使裂开的两项之差和系数之积与原通项相等．如：若{an}是等差数列，则1anan＋1＝1d1an－1an＋1，1anan＋2＝12d1an－1an＋2．[演

练冲关](2016·石家庄一模)已知等差数列{an}中，2a2＋a3＋a5＝20，且前10项和S10＝100．(1)求数列{an}的通项公式；(2)若bn＝1anan＋1，求数列{bn}的前n项和．解：(

1)由已知得2a2＋a3＋a5＝4a1＋8d＝20，10a1＋10×92d＝10a1＋45d＝100，解得a1＝1，d＝2.∴{an}的通项公式为an＝1＋2(n－1)＝2n－1．(2)bn＝12n－12n＋1＝1212n－1

－12n＋1，∴数列{bn}的前n项和Tn＝121－13＋13－15＋„＋12n－1－12n＋1＝12×1－12n＋1＝n2n＋1．板块命题点专练（八）点击此处