【文档说明】高考数学(文数)一轮复习课件 第八章 解析几何 第四节 直线与圆、圆与圆的位置关系(含详解).ppt，共(26)页，543.000 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-33625.html

以下为本文档部分文字说明：

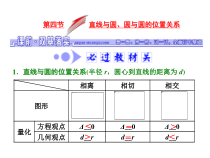
第四节直线与圆、圆与圆的位置关系相离相切相交图形量化方程观点Δ__0Δ__0Δ__0几何观点d__rd__rd__r＜＞＝＝＞＜1．直线与圆的位置关系(半径r，圆心到直线的距离为d)相离外切相交内切内含图形量的关系___________________

_________________________________d＞r1＋r2d＝r1＋r2|r1－r2|＜d＜r1＋r2d＝|r1－r2|d＜|r1－r2|2．圆与圆的位置关系(两圆半径r1，r2，d＝|O1O2|)1．圆(x＋2)2＋y2＝4与圆(

x－2)2＋(y－1)2＝9的位置关系为()A．内切B．相交C．外切D．相离[小题体验]解析：两圆圆心分别为(－2,0)，(2,1)，半径分别为2和3，圆心距d＝42＋12＝17．∵3－2<d<3＋2，∴两圆相交．答案：B2．直线l：3x－y－6＝0与圆x2＋y2－2x

－4y＝0相交于A，B两点，则|AB|＝________．解析：由x2＋y2－2x－4y＝0，得(x－1)2＋(y－2)2＝5，所以该圆的圆心坐标为(1,2)，半径r＝5，又圆心(1,2)到直线3x－y－6＝0的距离为d＝|3－2－

6|32＋－12＝102，由|AB|22＝r2－d2，得|AB|2＝45－52＝10，即|AB|＝10．答案：103．(教材习题改编)若直线x－y＋1＝0与圆(x－a)2＋y2＝2有公共点，则实数a的取值范围为________．解析

：由题意可得，圆的圆心为(a,0)，半径为2，∴|a－0＋1|12＋－12≤2，即|a＋1|≤2，解得－3≤a≤1．答案：[－3,1]1．对于圆的切线问题，尤其是圆外一点引圆的切线，易忽视切线斜率

k不存在的情形．2．两圆相切问题易忽视分两圆内切与外切两种情形．1．过点(2,3)与圆(x－1)2＋y2＝1相切的直线的方程为________．[小题纠偏]解析：①若切线的斜率存在时，设圆的切线方程为y＝k

(x－2)＋3，由圆心(1,0)到切线的距离为半径1，得k＝43，所以切线方程为4x－3y＋1＝0，②若切线的斜率不存在，则切线方程为x＝2，也是圆的切线，所以直线方程为4x－3y＋1＝0或x＝2．答案：x＝2或4x－3y＋1＝02．若圆x2＋y2＝1与圆(x＋4)2＋(y－a

)2＝25相切，则常数a＝________．答案：±25或0考点一直线与圆的位置关系[题组练透]1．圆(x－1)2＋(y＋2)2＝6与直线2x＋y－5＝0的位置关系是()A．相切B．相交但直线不过圆心C．相交过圆心D．相离解析：由题意知圆心(1，－2)到直线2x

＋y－5＝0的距离d＝|2×1－2－5|22＋12＝5＜6且2×1＋(－2)－5≠0，所以直线与圆相交但不过圆心．答案：B2．(2017·聊城模拟)圆(x－3)2＋(y－3)2＝9上到直线3x＋4y－11＝0的距离等于1的点的个数为()A．1B

．2C．3D．4解析：因为圆心到直线的距离为|9＋12－11|5＝2，又因为圆的半径为3，所以直线与圆相交，由数形结合知，圆上到直线的距离为1的点有3个．答案：C3．圆x2＋y2＝1与直线y＝kx＋2没有

公共点的充要条件是________．解析：法一：将直线方程代入圆的方程，得(k2＋1)x2＋4kx＋3＝0，直线与圆没有公共点的充要条件是Δ＝16k2－12(k2＋1)＜0，解得k∈(－3，3)．法二：圆心(0,0)到直线y＝kx＋2的距离d＝2k2＋1，直线与圆没有公共点的充要条件是d＞1，即

2k2＋1>1，解得k∈(－3，3)．答案：k∈(－3，3)[谨记通法]判断直线与圆的位置关系一般有两种方法(1)几何法：圆心到直线的距离与圆半径比较大小，即可判断直线与圆的位置关系．这种方法的特点是计算量较小．(2)代数法：将直线方程与圆方程联立方程组，再将二次

方程组转化为一元二次方程，该方程解的情况即对应直线与圆的位置关系．这种方法具有一般性，适合于判断直线与圆锥曲线的位置关系，但是计算量较大，能用几何法，尽量不用代数法．考点二切线、弦长问题与圆有关的切线及弦长问题，是近年来

高考的一个热点，常见的命题角度有：(1)求圆的切线方程(切线长)；(2)求弦长；(3)由弦长及切线问题求参数．[锁定考向][题点全练]角度一：求圆的切线方程(切线长)1．已知圆的方程为x2＋y2＝1，则在y轴上截距为2的切线方程为()A．y＝x＋2B．y＝－x＋2C．y＝x＋2

或y＝－x＋2D．x＝1或y＝x＋2解析：在y轴上截距为2且斜率不存在的直线显然不是切线，故设切线方程为y＝kx＋2，则|2|k2＋1＝1，所以k＝±1，故所求切线方程为y＝x＋2或y＝－x＋2．答案：C角度二：求弦长2．若a2＋b2＝2c

2(c≠0)，则直线ax＋by＋c＝0被圆x2＋y2＝1所截得的弦长为()A．12B．1C．22D．2解析：因为圆心(0,0)到直线ax＋by＋c＝0的距离d＝|c|a2＋b2＝|c|2|c|＝22，因此根据直角三角形的关系，弦长的一半就等于1－222＝

22，所以弦长为2．答案：D角度三：由弦长及切线问题求参数3．(2017·重庆适应性测试)已知圆C：(x－1)2＋(y－2)2＝2截y轴所得线段与截直线y＝2x＋b所得线段的长度相等，则b＝()A．－6B．±6

C．－5D．±5解析：记圆C与y轴的两个交点分别是A，B，由圆心C到y轴的距离为1，|CA|＝|CB|＝2可知，圆心C(1,2)到直线2x－y＋b＝0的距离也等于1才符合题意，于是|2×1－2＋b|5＝1，解得b＝±5，选D．答案：D[通法在握]1．圆的切线方程的2种求法(1)代数法：设切线方

程为y－y0＝k(x－x0)，与圆的方程组成方程组，消元后得到一个一元二次方程，然后令判别式Δ＝0进而求得k．(2)几何法：设切线方程为y－y0＝k(x－x0)，利用点到直线的距离公式表示出圆心到切线

的距离d，然后令d＝r，进而求出k．[提醒]若点M(x0，y0)在圆x2＋y2＝r2上，则过M点的圆的切线方程为x0x＋y0y＝r2．2．弦长的2种求法(1)代数法：将直线和圆的方程联立方程组，消元后得到一个一元二次方程．在判别式Δ＞0的前提下，利用根与系数的关系，根据弦长公式求弦长

．(2)几何法：若弦心距为d，圆的半径长为r，则弦长l＝2r2－d2．[演练冲关]1．(2017·湖南四地联考)若圆C：x2＋y2＋2x－4y＋3＝0关于直线2ax＋by＋6＝0对称，过点(a，b)作圆的切线，则切线长的最小值是()A．2B．3C．4D．6解析：圆C的标准

方程为(x＋1)2＋(y－2)2＝2，所以圆心为点(－1,2)，半径为2．因为圆C关于直线2ax＋by＋6＝0对称，所以圆心C在直线2ax＋by＋6＝0上，所以－2a＋2b＋6＝0，即b＝a－3，点(a，b)到圆心的距离d＝a＋12＋b－22＝a＋1

2＋a－3－22＝2a2－8a＋26＝2a－22＋18．所以当a＝2时，d取最小值18＝32，此时切线长最小，为322－22＝16＝4，所以选C．答案：C2．(2017·山西三地五校联考)过原点且与直线6x－3y＋

1＝0平行的直线l被圆x2＋(y－3)2＝7所截得的弦长为________．解析：由题意可得l的方程为2x－y＝0，∵圆心(0，3)到l的距离d＝33＝1，∴所求弦长l＝2R2－d2＝27－1＝26．答案：26考点三圆与圆的

位置关系[典例引领](2016·山东高考)已知圆M：x2＋y2－2ay＝0(a＞0)截直线x＋y＝0所得线段的长度是22，则圆M与圆N：(x－1)2＋(y－1)2＝1的位置关系是()A．内切B．相交C．外切D．相离解析：法一：由x2

＋y2－2ay＝0，x＋y＝0，得两交点为(0,0)，(－a，a)．∵圆M截直线所得线段长度为22，∴a2＋－a2＝22．又a>0，∴a＝2．∴圆M的方程为x2＋y2－4y＝0，即x2＋(y－2)2＝4，圆心M(0,2)，半径r1＝2．又圆N：(x－1)2＋(y－1)2＝1，圆心N(1

,1)，半径r2＝1，∴|MN|＝0－12＋2－12＝2．∵r1－r2＝1，r1＋r2＝3,1<|MN|<3，∴两圆相交．法二：由题知圆M：x2＋(y－a)2＝a2(a＞0)，圆心(0，a)到直线x＋y＝0的距离d＝a2，所以2a

2－a22＝22，解得a＝2．圆M，圆N的圆心距|MN|＝2，两圆半径之差为1，故两圆相交．答案：B[由题悟法]解决圆与圆位置关系问题的2大通法(1)处理两圆位置关系多用圆心距与半径和或差的关系判断，一般不采用

代数法．(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差得到．[即时应用]1．(2017·山西太原模拟)若圆C1：x2＋y2＝1与圆C2：x2＋y2－6x－8y＋m＝0外切，则m＝()A．21B．19C

．9D．－11解析：圆C1的圆心为C1(0,0)，半径r1＝1，因为圆C2的方程可化为(x－3)2＋(y－4)2＝25－m，所以圆C2的圆心为C2(3,4)，半径r2＝25－m(m＜25)．从而|C1C2|＝32＋42＝5．由两圆外切得|C1C2|＝r1＋r2，即1＋25－m＝

5，解得m＝9，故选C．答案：C2．若圆x2＋y2＝4与圆x2＋y2＋2ay－6＝0(a＞0)的公共弦长为23，则a＝________．解析：方程x2＋y2＋2ay－6＝0与x2＋y2＝4．两式相减得：2

ay＝2，则y＝1a．由已知条件22－32＝1a，即a＝1．答案：1板块命题点专练（十二）点击此处