【文档说明】2023年人教版数学七年级下册期末复习《平行线的性质与判定》解答题专项复习(含答案).doc，共(13)页，246.459 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-243253.html

以下为本文档部分文字说明：

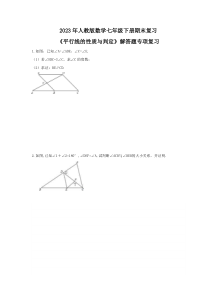
2023年人教版数学七年级下册期末复习《平行线的性质与判定》解答题专项复习1.如图，已知∠A=∠ADE，∠C=∠E.（1）若∠EDC=3∠C，求∠C的度数；（2）求证：BE∥CD.2.如图,已知∠1＋∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系，并证明.3.如

图，△ABC中，∠ACB=90°，CD⊥AB，点D为垂足，点E，F分别在AC．AB边上，且∠AEF=∠B．求证：EF∥CD．4.如图,已知D是BC上的一点,DE∥AC,DF∥AB．求证:∠A＋∠B＋∠C=180°．5.如图，已知BE∥DF，∠B＝∠D,试说明AD∥BC.6.如图，

CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1=∠2，∠3=80°．（1）试证明∠2=∠DCB；（2）试证明DG∥BC；（3）求∠BCA的度数．7.如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上

，EF⊥AB，垂足为F．（1）CD与EF平行吗？为什么？（2）如果∠1=∠2，那么DG∥BC吗？为什么？8.如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．9.如图,已知DE⊥AO于点E,BO⊥AO于点

O,∠CFB=∠EDO.证明：CF∥DO．10.已知直线，直线与直线、分别相交于C、D两点．（1）如图a，有一动点P在线段CD之间运动(不与C、D两点重合)，问在点P的运动过程中，是否始终具有∠3+∠1=∠

2这一关系，为什么？（2）如图b，当动点P线段CD之外运动(不与C、D两点重合)，问上述结论是否成立?若不成立，试写出新的结论并说明理由．11.如图，已知DG⊥BC,AC⊥BC，EF⊥AB,∠1=∠2.求证：CD⊥AB.12.如图，已知∠ABC+∠ECB=180°，∠P=∠Q．求证

：∠1=∠2．13.已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由.（2）当点P在C、D两点的外侧运动时（P点与

点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由.14.如图,已知∠1=∠2，∠3=∠4，∠5=∠6.求证：ED∥FB．15.已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.(

1)如图1,若∠E＝80°,求∠BFD的度数.(2)如图2,若∠ABM＝13∠ABF,∠CDM＝13∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.(3)若∠ABM＝1n∠ABF,∠CDM＝1n∠C

DF,∠E＝m°,请直接用含有n,m°的代数式表示出∠M.16.如图1，直线MN与直线AB.CD分别交于点E.F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD

的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否

发生变化？若不变，请求出其值；若变化，说明理由．答案1.证明：（1）∵∠A=∠ADE，∴AC∥DE.∴∠EDC＋∠C=180°.又∵∠EDC=3∠C，∴4∠C=180°.即∠C=45°.（2）证明：∵AC∥DE，∴∠E=∠ABE.又∵∠C=∠E，∴∠C=∠ABE.∴BE

∥CD.2.解：∠ACB与∠DEB相等，理由如下：证明：∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义），∴∠2=∠DFE（同角的补角相等），∴AB∥EF（内错角相等两直线平行），∴∠BDE=∠DEF（两

直线平行，内错角相等），∵∠DEF=∠A（已知），∴∠BDE=∠A（等量代换），∴DE∥AC（同位角相等两直线平行），∴∠ACB=∠DEB（两直线平行，同位角相等）．3.证明：∵∠ACB=90°，∴∠B+∠A=90°，∵CD

⊥AB，∴∠ADC=90°，∴∠A+∠ACD=90°，∴∠B=∠ACD，∵∠AEF=∠B，∴∠AEF=∠ACD，∴EF∥CD．4.证明：∵DE∥AC（已知），∴∠BED＝∠A，∠BDE＝∠C（两直线平行

，同位角相等）．∵DF∥AB（已知），∴∠BED＝∠EDF（两直线平行，内错角相等），∠FDC＝∠B（两直线平行，同位角相等）．∴∠EDF＝∠A（等量代换）．∵∠BDE＋∠EDF＋∠FDC＝180°（平角定

义），∴∠C＋∠A＋∠B＝180°（等量代换）．即∠A＋∠B＋∠C＝180°．5.证明：∵BE∥DF(已知)，∴∠B＋∠BCD＝180°(两直线平行，同旁内角互补)∵∠B＝∠D(已知)∴∠D＋∠BCD＝180°(等量代换)

∴AD∥BC(同旁内角互补,两直线平行)6.（1）证明：∵CD⊥AB于D，FE⊥AB，∴CD∥EF，∴∠2=∠DCB（2）证明：∵∠2=∠DCB，∠1=∠2，∴DG∥BC（3）解：∵DG∥BC，∠3=80°，∴∠BCA=∠3=80°7.解：（1）CD∥EF，理由是

：∵CD⊥AB，EF⊥AB，∴∠CDF=∠EFB=90°，∴CD∥EF．（2）DG∥BC，理由是：∵CD∥EF，∴∠2=∠BCD，∵∠1=∠2，∴∠1=∠BCD，∴DG∥BC．8.解：∵EF∥AD，AD∥BC，∴E

F∥BC，∴∠ACB+∠DAC=180°，∵∠DAC=120°，∴∠ACB=60°，又∵∠ACF=20°，∴∠FCB=∠ACB﹣∠ACF=40°，∵CE平分∠BCF，∴∠BCE=20°，∵EF∥BC，∴∠FEC=∠ECB，∴∠

FEC=20°．9.证明：∵DE⊥AO，BO⊥AO，∴∠AED=∠AOB=90°，∴DE∥BO（同位角相等，两条直线平行），∴∠EDO=∠BOD（两直线平行，内错角相等），∵∠EDO=∠CFB，∴∠B

OD=∠CFB，∴CF∥DO（同位角相等，两条直线平行）．10.解：（1）作PE∥，则∠1=∠APE∵，∴PE∴∠3=∠BPE∵∠APB=∠APE+∠BPE∴∠APB=∠1+∠3（2）上述结论不成立．新结论：∠1=∠2+∠3∵，∴∠1=∠AFB∵∠AFB=∠2+∠3∴∠1=∠

2+∠3.11.证明：∵∴‖∴∵∴∴‖∵∴∴∴12.证明：∵∠ABC+∠ECB=180°，∴AB∥DE，∴∠ABC=∠BCD，∵∠P=∠Q，∴PB∥CQ，∴∠PBC=∠BCQ，∵∠1=∠ABC﹣∠PBC，∠2=∠BCD﹣∠BCQ，∴∠1=∠2．13.解：（1）∠APB=∠PAC+∠PBD

；过点P作PE∥L1∴∠APE=∠PAC-∵L1∥L2∴PE∥L2∴∠BPE=∠PBD∴∠APE+∠BPE=∠PAC+∠PBD∴∠APB=∠PAC+∠PBD(2)不成立；图2：∠PAC=∠APB+∠PBD；图3：∠PBD=∠P

AC+∠APB；14.证明：∵∠3=∠4,∴AC∥BD.∴∠6+∠2+∠3=180°.∵∠6=∠5，∠2=∠1,∴∠5+∠1+∠3=180°.∴ED∥FB.15.解：（1）如图，作EG∥AB，FH∥AB，∵AB∥CD，∴EG∥AB∥FH∥CD，∴∠ABF＝∠BFH

，∠CDF＝∠DFH，∠ABE＋∠BEG＝180°，∠GED＋∠CDE＝180°，∴∠ABE＋∠BEG＋∠GED＋∠CDE＝360°∵∠BED＝∠BEG＋∠DEG＝70°，∴∠ABE＋∠CDE＝290°，∵∠A

BF和∠CDF的角平分线相交于E，∴∠ABF＋∠CDF＝145°，∴∠BFD＝∠BFH＋∠DFH＝145°；（2）∵∠ABM＝13∠ABF，∠CDM＝13∠CDF，∴∠ABF＝3∠ABM，∠CDF＝3∠CDM，∵∠ABE与∠CD

E两个角的角平分线相交于点F，∴∠ABE＝6∠ABM，∠CDE＝6∠CDM，∴6∠ABM＋6∠CDM＋∠E＝360°，∵∠M＝∠ABM＋∠CDM，∴6∠M＋∠E＝360°．(3)由(2)结论可得，2n∠ABN＋2n∠CDM＋∠E＝360°，∠M＝∠AB

M＋∠CDM，解得：∠M＝错误!未找到引用源。．故答案为：∠M＝错误!未找到引用源。.16.（1）解：如图1∵∠1与∠2互补，∴∠1+∠2=180°．又∵∠1=∠AEF，∠2=∠CFE，∴∠AEF+∠CFE=180°，∴AB∥CD（2）解：如图2，由（1）

知，AB∥CD，∴∠BEF+∠EFD=180°．又∵∠BEF与∠EFD的角平分线交于点P，∴∠FEP+∠EFP=0.5（∠BEF+∠EFD）=90°，∴∠EPF=90°，即EG⊥PF．∵GH⊥EG，∴PF∥GH（3）解：∠HPQ的大小不发生变化，理由如下：如图3，

∵∠1=∠2，∴∠3=2∠2．又∵GH⊥EG，∴∠4=90°-∠3=90°-2∠2．∴∠EPK=180°-∠4=90°+2∠2．∵PQ平分∠EPK，∴∠QPK=0.5∠EPK=45°+∠2．∴∠HPQ=∠QPK-∠2=45°，∴∠HPQ的大小不发生变化，一直是45°