【文档说明】青岛版数学七年级下册课时练习9.3《平行线的性质》(含答案) .doc，共(7)页，178.059 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-181155.html

以下为本文档部分文字说明：

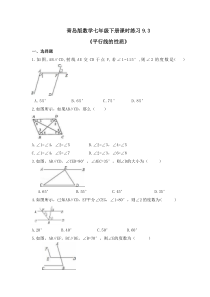
青岛版数学七年级下册课时练习9.3《平行线的性质》一、选择题1.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是（）A.55°B.65°C.75°D.85°2.如图所示，如果AB∥CD，

那么（）A.∠1=∠4，∠2=∠5B.∠2=∠3，∠4=∠5C.∠1=∠4，∠5=∠7D.∠2=∠3，∠6=∠83.如图，AB∥CD，∠CED=90°，∠AEC=35°，则∠D的大小为（）A.65°B.55°C.45°D.35°4.如图所示

，已知AB∥CD，EF平分∠CEG，∠1=80°，则∠2的度数为()A.20°B.40°C.50°D.60°5.如图，AB∥EF，BC∥DE，∠B=70°，则∠E的度数为（）A.90°B.110°C.130°D.160°6.如图,已知AB∥C

D,BC平分∠ABE,∠C=33°,则∠CEF的度数是（）A.16°B.33°C.49°D.66°7.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=35°,那么∠B的度数为（）A.35°B.45°C.55°D.145°8.如图,AB∥CD∥EF,BC∥AD

,AC平分∠BAD,则图中与∠AGE相等的角（）A.2个B.3个C.4个D.5个9.如图，把一块含有30°角(∠A=30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个

顶点F与三角板斜边相交于点F，如果∠1=40°,那么∠AFE=（）A.50°B.40°C.20°D.10°10.如图，AB∥CD,FE⊥DB,垂足为E，∠1=50°，则∠2的度数是（）A.60°B.50°C.40°D.30°二、填空题11.如图，若AB∥CD，则在图中所标注的角中，一定相等

的角是．12.如图，点D、E分别在AB、BC上，DE∥AC，AF∥BC，∠1=70°，则∠2=°．13.如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C=度．14.如图,直线l1、l2分别与直线l3、l4相交,∠1与∠3互余,∠3余角与∠

2互补,∠4=125°,则∠3=______．15.如图,已知直线AB∥CD,直线EG垂直于AB,垂足为G,直线EF交CD于点F,∠1=50°,则∠2=．16.如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数，下面给出了求∠

AGD的度数的过程，将此补充完整并在括号里填写依据．【解】∵EF∥AD（已知）∴∠2=_________（）又∵∠1=∠2（已知）∴∠1=∠3（等式性质或等量代换）∴AB∥_________（）∴∠BAC+_________=180°（）又∵∠BAC=70°（已

知）∴∠AGD=_________（）三、解答题17.如图，直线a∥b，三角形纸板的直角顶点A落在直线a上，两条直线分别交直线b于B，C两点.若∠1=42°，求∠2的度数.18.如图，AB∥CD，∠ACB＝90°，∠ACD＝55°，求∠B的度数.19.如图,已知AB∥CD,EF交AB于

G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=500.求∠BHF的度数．20.如图，在△ABC中，D，E，F分别为AB，AC，BC上的点，且DE∥BC，EF∥AB.求证：∠ADE=∠EFC.21.如图.AB∥CD∥PN.∠ABC=

50°,∠CPN=150°.求∠BCP的度数．参考答案1.B2.D3.B4.C5.B6.D7.C8.D9.C10.C11.答案为：∠1=∠3．12.答案为：70．13.答案为：6514.答案为：55°．15.答案为：

14016.答案为：∠3，两直线平行，同位角相等，DG，内错角相等，两直线平行，∠AGD，两直线平行，同旁内角互补，100°，等式性质．17.解：∵直线a∥b，∠1=42°(已知)，∴∠ACB=42°(两直线平行，内错角相等).又∵∠BAC=90°(已知)，∴∠ABC=180°－∠

BAC－∠ACB=48°(三角形的内角和为180°)，∴∠2=∠ABC=48°(对顶角相等).18.解：∠B＝35°.因为AB∥CD，所以∠A＝∠ACD＝55°，在Rt△ABC中，因为∠A＝55°，所以∠B＝90°－55°＝35°19.

略20.证明：∵DE∥BC(已知)，∴∠ADE=∠B(两直线平行.同位角相等).又∵EF∥AB(已知)，∴∠EFC=∠B(两直线平行，同位角相等).∴∠ADE=∠EFC(等量代换).21.由AB∥CD，∠ABC＝50°可得∠BCD＝50°．由PN∥CD，∠CPN＝15

0°，可得∠PCD＝30°．∴∠BCP＝∠BCD－∠PCD＝50°－30°＝20°．