【文档说明】浙教版数学七年级下册课时练习1.4《平行线的性质》(含答案).doc，共(7)页，190.953 KB，由MTyang资料小铺上传

转载请保留链接：https://www.ichengzhen.cn/view-156731.html

以下为本文档部分文字说明：

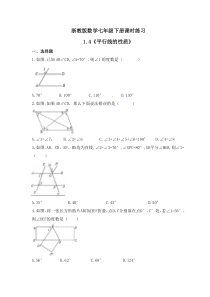
浙教版数学七年级下册课时练习1.4《平行线的性质》一、选择题1.如图,已知AB∥CD,∠A=70°,则∠1的度数是（）A.70°B.100°C.110°D.130°2.如图,如果AB∥CD，那么下面说法错误的是（）A.∠3=∠7；B.∠2=∠6C.∠3+∠4+∠5+

∠6=1800D.∠4=∠83.如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=（）A.35°B.40°C.45°D.50°4.如图，将一张长方形纸片ABCD沿EF折叠，点D

、C分别落在点D′、C′处，若∠1=56°，则∠DEF的度数是（）A.56°B.62°C.68°D.124°5.如图，DH∥EG∥BC，且DC∥EF，那么图中和∠1相等的角有（）个．A.2B.4C.5D.66.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,

则∠CEF的度数是（）A.16°B.33°C.49°D.66°7.如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于（）A.90°B.180°C.210°D.270°8.一辆汽车在公路上行驶

,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是()A.先向左转130°，再向左转50°B.先向左转50°，再向右转50°C.先向左转50°，再向右转40°D.先向左转50°，再向左转

40°9.如图，直线AE∥CD，∠EBF=135°，∠BFD=60°，则∠D等于()A.75°B.45°C.30°D.15°10.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=(180-a)°；②OF平分∠BOD；③∠POE

=∠BOF；④∠POB=2∠DOF.其中正确的个数有多少个?（）A.1B.2C.3D.4二、填空题11.如图，若AB∥CD，则在图中所标注的角中，一定相等的角是．12.如图,直线a//b，直线c与a,b相交

.若1=70°，则2=．13.如图,在△ABC中,DE∥BC,EF∥AB,则∠B相等的角有______个。14.将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=°．15.如图，AB∥CD，若∠ABE=120°，∠DCE=32°，则∠BEC=．16.如图1是长方形纸袋,∠D

EF=a,将纸袋沿EF折叠成图2,在沿BF折叠成图3,用表示图3中∠CFE的大小为_________三、解答题17.如图，AB∥CD，∠ACB＝90°，∠ACD＝55°，求∠B的度数.18.如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．

19.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数．20.如图，已知∠A=∠ADE，∠C=∠E.（1）若∠EDC=3∠C，求∠C的度数；（2）求证：BE∥CD.21.如图,已知∠1=∠2，∠3=∠4，∠5=∠6.求证：ED∥FB．22.如图,已知△ABC．求

证：∠A＋∠B＋∠C=180°．参考答案1.C2.D3.D4.B5.C6.B7.D.8.C.9.D10.C11.答案为：∠1=∠3．12.答案为：70°13.答案为：314.答案为：110°．15.答案为：92°．16.答案为：180°﹣3α．1

7.解：∠B＝35°.因为AB∥CD，所以∠A＝∠ACD＝55°，在Rt△ABC中，因为∠A＝55°，所以∠B＝90°－55°＝35°18.解：∵AB∥CD，∴∠B+∠BCE=180°（两直线平行，同旁内角互补）.∵∠B=65°，∴∠BCE=115°.∵CM平分∠BCE，∴∠ECM=0.

5∠BCE=57.5°.∵∠ECM+∠MCN+∠NCD=180°，∠MCN=90°，∴∠NCD=180°-∠ECM-∠MCN=180°-57.5°-90°=32.5°．19.解：∵AB∥CF，∠ABC=70°，∴∠BCF=∠ABC=70°，又∵DE∥CF，∠CDE=

130°，∴∠DCF+∠CDE=180°，∴∠DCF=50°，∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°．20.（1）∵∠A=∠ADE，∴AC∥DE.∴∠EDC＋∠C=180°.又∵∠EDC=3∠C，∴4∠C=180°.即∠C=4

5°.（2）证明：∵AC∥DE，∴∠E=∠ABE.又∵∠C=∠E，∴∠C=∠ABE.∴BE∥CD.21.证明：∵∠3=∠4,∴AC∥BD.∴∠6+∠2+∠3=180°.∵∠6=∠5，∠2=∠1,∴∠5+∠1+∠3=180°.∴ED∥FB.22.证明：如图，延长BC到D，过点C作CE∥BA

，∵BA∥CE，∴∠B=∠1（两直线平行，同位角相等），∠A=∠2（两直线平行，内错角相等），又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），∴∠A+∠B+∠ACB=180°（等量代换）．