【文档说明】《全等三角形判定的应用》教学设计1-八年级上册数学北京版.docx，共(8)页，5.648 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-23390.html

以下为本文档部分文字说明：

教学课题全等三角形的实际应用教学目标1.让学生进一步巩固判定三角形全等的方法，培养学生的理性思考和逻辑推理能力；2.让学生经历构造全等三角形解决实际问题的过程，培养学生的数学建模能力和语言表达能力；3.让学生感受数学与实际的广泛、密切联系，体会数学说理的严谨、数学应用的价值，激发学生学习的兴趣和信

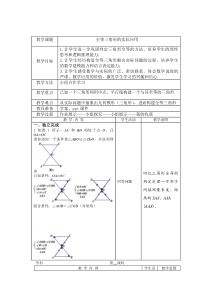
心.教学方法小组合作学习教学重点已知一个三角形利用中点，平行线构建一个与其全等的三角形教学难点从实际问题中抽象出几何模形（三角形），进而构建全等三角形教具准备学案，ppt课件教学过程作业展示——小组探究——小组展示——我的收获教

学内容学生活动教学意图一、独立完成1.如图1所示，AC和BD相较于点O，且OA=OC请你添加一个条件使△ABO≌△CDO，并说明理由.已知条件：OA=OC隐含条件：∠AOB＝∠COD（对顶角）回答问题回忆三角形全等的判定定理—可用于间接测量长度、距离的SAS、ASA(A

AS)，学科第课时教学内容学生活教学意图动2.在图2和图3中分别画△ABO的一个全等三角形，并说明理由.课前完成个人展示熟悉全等三角形的构造方法(平移、翻折、旋转)，为本节课的重点内容，也是本节课解决实际问题的关键学生经常做出一种方法之后就不再思考了，有“知足常乐

”的思想，这也是“懒惰”的一种表现，这在学习上不可取的，要培养学生发散思维，从多角度去思考问题，并从中进行比较，寻找最优方案学科第课时教学内容学生活动教学意图二、小组探究1.解决“炮楼距离”问题在“砥砺奋进的五年”大型成就展中有一个展区是实现强军目标，建设世界一流军队，和平年代军队的作用

至关重要，在民族解放的战争年代，军队更是做出了重大贡献，这是一个发生在抗日战争期间的故事：为了炸毁与我军阵地隔河相望的敌人炮楼，需要测量我军阵地到敌人炮楼的距离；由于没有任何测量工具，八路军战士为此绞尽脑汁；一位聪明的战士想出了一个巧妙的办法，成功地测出了距离而炸毁了碉堡。他

是这样做的：先利用军帽使自己的视线正好落在敌人炮楼的位置；再转过身，保持刚才的视线，看目光落在什么位置；然后步测出这段距离，就是我军阵地与敌人炮楼的距离，（1）你能用全等三角形知识来解释吗？（2）你还有其他的方式吗？有几种解法？2.解决“池塘宽度”问题上周末，小明和朋友们游览风

景区，看到了一个美丽的池塘。他们想知道池边两点Ａ、Ｂ之间的距离，但是只有测角仪和尺子，没有船。他们应该怎么办呢？你有几种方法？课上完成组内交流小组展示由于学生没有实际经验，他们的知识大多停留在书本上，所以

通过设计给出战士的具体做法，让学生站在战士的角度，将实际问题自己抽象出几何模型，进而解决问题，同时也是给他们一个解决问题的思路，从而可以思考还可以怎样解决问题，给学生一个台阶，从而引发他们的思考这个问题更接近学生实际，在上一个问题的基础上，可以很容易得到解决，但同时这两个问

题也有不同的地方，需要学生自己去发现，进而会得到不一样的解决方案，但学生很容易局限在第一个问题当中，所以要培养学生的发散思维学科第课时教学内容学生活动教学意图三、小组展示1.解决“炮楼距离”问题细心的同学会发现，战士的做法恰恰利用了我们刚才的构建全等三角形的方法，但前

提是先自己找思考写出解答过程讲解思路展示到一个三角形，也就是在实际问题中抽象出一个三角形，不共线三点即可构成三角形，首先明确要测量的对象，即可确定两个点，再确定一个点，进而通过构建全等三角形，将不可测量的对象转化为可测量的对象，从而解决问题，锻炼表达能力，

树立将所遇到的问题转化为所学知识上，学有所用，同时深化对所学知识的理解学生再结合我们开始让他们自己构建全等三角形的方法，会想到其他的三种方案学科第课时教学内容学生活动教学意图三、小组展示2.解决“池塘宽度”问题讲解思路展示首先检查学生对上

一问题的理解，他们能不能用上一个问题的解决思路来设计其次学生在描述自己的方案时，他们更多的还是停留在纸面，没有考虑实际操作再次，正是因为有第一个问题，很多学生都会局限在此，方案1——方案4都是基于这种思路进行设计的，用的

都是ASA(AAS)方案5体现了这两个问题的不同，就是第一个问题构建三角形是只能测量一个边，用ASA(AAS)而第二个问题可以测量一个三角形中的两个边长，还可以用SAS来解决，主要培养学生的发散思维学科第课时教学内容学生活动教学意图四、我的收获1.已知三角形如

何利用中点、平行线构建全等三角形2.所学知识要用的解决实际问题，转化思想3.知识的发展需要我们这一代的努力五、课后作业1.公园里有一条Z字型道路ABCD，其中AB//CD，在AB和BC段的路边各有小石凳E和M，M恰为BC的中点，在AB

道路上停放着一排小汽车，从而无法直接测量B，E之间的距离，你能想出解决的方法吗?请说明其中的道理.2.一个学生要测量小口瓶下半部的内径，他用两根长度相等的钢条AA‘’、BB‘’在中点连在一起，可活动A、B两点。使A‘、B’卡在瓶的内壁上。然后量出AB间的长度，就可测量出小口瓶下半部

的内径，请说明为什么?总结发言课后完成对所学内容进行总结，一要养成习惯，二加深对所学内容的认识升华，三锻炼表达能力巩固所学加深理解3.如图，要测量AB的长，因为无法过河接近点A，可以在AB线外任取一点D，在AB的延长线上

任取一点E。连结ED和BD，并且延长BD到G．使DG=BD；延长ED到F，A使DF=ED．连结FG．并延长FG到，使H、D、A在一直线上，则HG=AB．试证明这种测量方法的原理是正确的．课后反思：通过这两个问题的探究学习，学生了解了全等三角形知识的实际应用，进一步理解了三角形全等的判定方法

，掌握全等三角形的构造方法；同时，在思考、推理、建模、表达和转换的过程中，学生也体会到了数学说理的严谨、数学应用的价值。而从学生的反馈中也可以看到，本节课中新鲜的材料、丰富的方案激活、拓宽了学生的思维，使学生在不知不觉中感受到数学与实际的广泛、密切联系，激发出学习的兴趣和信心。

但同时我也可以看到学生在思维的发散性上，表达能力上还存在不足，在后续的教学中注意这些方面的训练。