【文档说明】《等可能情形下概率的特征》PPT课件1-九年级下册数学沪科版.ppt，共(17)页，1.293 MB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-20400.html

以下为本文档部分文字说明：

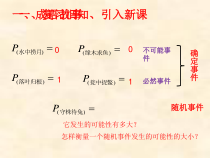
一、成语故事)(水中捞月P)(缘木求鱼P00)(守株待兔P)(落叶归根P)(瓮中捉鳖P11不可能事件必然事件确定事件随机事件它发生的可能性有多大？怎样衡量一个随机事件发生的可能性的大小？一、复习旧知、引入新课二、学习目标

：1、在解决实际问题的过程中，体会随机的思想，进一步理解概率的意义。2、理解等可能情形下的随机事件的概率，会运用列举法计算随机事件的概率。三、实验1.从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,有几种可能性,每种的可能性各是多少呢?2.掷一个骰子，向上

一面的点数共有几种可能，每种的可能性各是多少？1，2，3，4，51，2，3，4，5，6上面的试验中,都有两个共同的特点:1)在一次实验中,所有可能出现的不同结果是有限个.2)在一次实验中,各种不同结果的可能性相等.

我们可以通过列举所有可能的结果，具体分析后得出随机事件的概率.有限性等可能性解：袋中有3个球，随意从中抽一个球，虽然红色、白色球的个数不等，但每个球被选中的可能性相等。抽出的球共有三种可能的结果：红（1）、红（2）、白，这三种结果是“等可能”的。三个结果中有两个结果使事件A（抽得红球）发生

，所以抽得红球的概率是即:四、合作探究：例1袋中有3个球,2红1白，除颜色外，其余如材料、大小、质量等完全相同，随意从中抽出一个球，抽到红球的概率是多少？23变式1：袋中有9个球,2红7白呢？变式3：袋中有n个球,m红（n-m)白呢？变式2：袋中有n个球,2红（n-2)

白呢？92)(APn2)(APnm)(AP32)(AP一般地,如果在一次实验中,有n种可能的结果,并且这些结果发生的可能性相等,其中使事件A发生的结果数有m（m≤n）种,那么事件A发生的概率为:nmAP当A是必然事件时，m=n,P(A)=1；

当A是不可能事件时，m=0,P(A)=0.1)(0AP1)(0AP则一般地，对任何随机事件A，它的概率的取值范围为必然事件概率为1，不可能概率事件为0袋中有6个除颜色外完全相同的小球,其中2个白球,2个黑球,1个红球,1个黄球,从中任意摸出1个球,则P(白球)=__

___;P(黑球)=_____;P(红球)=______;P(黄球)=_______.口答：62nmAP31613161开始所有可能出现的结果第二枚第一枚例2抛掷两枚均匀的硬币,求两枚硬币都是正面朝上的概率所有可能出现的结果第二枚第一枚（像这样的图，我们称之为，它可以帮助我们不重复、

不遗漏地列出一次试验中所有可能出现的结果。）开始正反正反反正（正,正）（正,反）（反,正）（反,反）解：抛掷两枚硬币，向上一面的情况一共可能出现以下四种不同的结果：（正，正），（正，反），（反，正），（反

，反）由树状图知所有可能的结果有4种，其中两枚都是正面朝上有1种树状图设两枚硬币都是正面朝上的事件为A，则41)(AP变式：抛掷3枚均匀的硬币，那么3枚硬币都是正面朝上的概率？开始第一枚正反第二枚正反正反第三枚正反正反正反正反解：抛掷三枚硬币的结果用树状图来表示如下：由

树状图可知：共有8种结果，且每种结果出现的可能性相等，其中3枚硬币都是正面朝上的结果有1种设3枚硬币都是正面朝上的事件为A，则81)(AP开始男１男２女１女２男１男２女１女２男１男２女１女２男女'女''获演唱奖的获演奏奖的由于

共有１２种结果，且每种结果出现的可能性相等，其中２名都是女生的结果有４种，所以事件Ａ发生的概率为P(A)=4/12=1/3解：设两名领奖学生都是女生的事件为Ａ，两种奖项各任选１人的结果用“树状图”来表示。例3某班有1名男生、２名女

生在校文艺演出获演唱奖，另有2名男生、２名女生获演奏奖。从获演唱奖和演奏奖的学生中各任选１人去领奖，求两人都是女生的概率树状图有什么特点？（2）两步试验或两步以上试验.树状图能不重复不遗漏的列出一次试验所有可能出现的结果树状图主要适用于：（1）所有可能出现的结果数不多的试验.五、理解应用：、

1、口袋中放有3个红球和11个黄球，这两种球除颜色外没有任何区别.随机从口袋中任取一个球。取到红球或黄球的概率分别是多少？2、在组成单词“Probability”（概率）的所有字母中任意抽出一个字母，则取到字母”

b”的概率是多少？3、一间宿舍有4张分上下铺的单人床，可安排8名同学住宿。小明和小兵同住一间宿舍，因为小兵小，大家一致同意他睡下铺，其余同学通过抽签决定自己的床铺，那么小明抽到睡上铺的概率是多少？小明恰好睡到小兵上铺的概率是多少?五、理解应用：5、从一副没有大小王的扑克牌（共5

2张）中随机抽一张，问：（1）抽到黑桃K的概率；（2）抽到红桃的概率；（3）抽到Q的概率。4、如图，随机闭合开关S1、S2、S3中的两个，求能让灯泡发光的概率．六、小结：1、一个随机事件发生的概率P(A)的范围是什么？必

然事件、不可能事件的概率分别是多少？2、等可能条件下的概率有什么特征？3、树状图适用于怎样的随机事件？七、布置作业：必做题：116页复习题1、2选做题：抛掷一个骰子，它落地时向上的的数为①2的概率是多

少？②落地时向上的数是3的倍数的概率是多少？③点数为奇数的概率是多少？④点数大于2且小于5的数的概率是多少？