【文档说明】《阅读材料 从勾股定理到图形面积关系的拓展》课后习题-八年级上册数学浙教版.doc，共(2)页，145.000 KB，由小喜鸽上传

转载请保留链接：https://www.ichengzhen.cn/view-18524.html

以下为本文档部分文字说明：

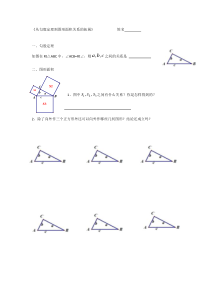
cbaS3S2S1BAC《从勾股定理到图形面积关系的拓展》姓名一、勾股定理如图在Rt△ABC中，∠ACB=Rt∠，则,,abc之间的关系是二、图形面积1、图中123,,sss之间有什么关系？你是怎样得到的？2、除了向外作三个正方形外还可以向外作哪些几何图形？结论还成立吗？S1S

2S3BACcbaS3S4S1S2ABC三、拓展1.2.四、应用练习1.如图,已知在Rt△ABC中,∠ACB=Rt∠，AB=4，分别以AC、BC为直径作半圆，面积分别记为S1、S2，则S1+S2的值等于.变式：若∠ABC=30°，则

S1+S2的值等于.练习2.如图，在Rt△ABC中，∠C=90°，分别以AB、AC、BC为边，在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4，若S正方形ABEF=25，S正方形ACPQ=

9，则S1+S2+S3+S4等于（）A.12B.15C.18D.20练习3.如图，在△ABC中，∠ACB＝90º，AC＞BC，分别以AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，连接EF、GM、ND，设△AEF、

△BND、△CGM的面积分别为S1、S2、S3，则下列结论正确的是（）A．S1＝S2＝S3B．S1＝S2＜S3C．S1＝S3＜S2D．S2＝S3＜S1练习4.已知：如图，以Rt△ABC的三边a、b、c为边分别向外作等腰直角三角形．面积分别为S1、S2、S3，若斜边AB＝6，则S1+S2为．

S1S2BACS2S1S3S4EFPQBAC