【文档说明】2-6功和能机械能守恒定律.pptx，共(48)页，924.776 KB，由精品优选上传

转载请保留链接：https://www.ichengzhen.cn/view-260341.html

以下为本文档部分文字说明：

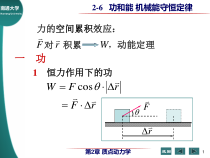
第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回一功力的空间累积效应：WrF，动能定理对积累1恒力作用下的功rFrFW==cosrF1第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回rFW

dcosd=FrdiF1drirdB**i1A1F2变力的功rFWdd===BABAsFrFWdcosdrsdd=sFWdcosd=功的单位（焦耳）mN1J1=2第2章质点动力学2-6功和能机械能守恒定律

南通大学NantongUniversity返回0d,900ooW0d,18090ooW0dd90o=⊥=WrF(1)功的正、负讨论(2)作功的图示cosF1s2ssdsosFWssdcos21=3第2章质点动力学2-6功和能机

械能守恒定律南通大学NantongUniversity返回（3）功是一个过程量，与路径有关．（4）合力的功，等于各分力的功的代数和．）（zddddzyBAxBAFyFxFrFW++==xFWBAxxxxd=z

WWWWyx++=kFjFiFFzyx++=kjyixrzdddd++=yFWBAyyyyd=zzzd=BAzzFW4第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回一个质点同时在几个力

作用下的位移为：(SI)，其中一个力为恒力(SI)，则此力在该位移过程中所作的功为(A)-67J．(B)17J．(C)67J．(D)91J．讨论1kjir654+−=kjiF953+−−=5第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUni

versity返回•某质点在力＝(4＋5x)(SI)的作用下沿x轴作直线运动，在从x＝0移动到x＝10m的过程中，力所做的功为__________．讨论2答案：290J6第2章质点动力学2-6功和能机械能守恒定律南通大学NantongU

niversity返回tWP=平均功率瞬时功率v===→FtWtWPtddΔΔlim0cosvFP=功率的单位（瓦特）W10kW13=1sJ1W1−=二功率7第2章质点动力学2-6功和能机械能守恒定律南通大学Na

ntongUniversity返回如图所示，木块m沿固定的光滑斜面下滑，当下降h高度时，重力作功的瞬时功率是：(A)．(B)．(C)．(D)．讨论3hm21)2(ghmg21)2(cosghmg21)21(singhmg21)2(singhmg8第2章

质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回例1一质量为m的小球竖直落入水中，刚接触水面时其速率为．设此球在水中所受的浮力与重力相等，水的阻力为,b为一常量.求阻力对球作的功与时间的函数关系．0vvbF−=r0vxo9第2章质点动力学2-6功和能机械能守恒

定律南通大学NantongUniversity返回解建立如右图所示的坐标系xbrFWdd−==v又由2-3节例5知tmb−=e0vvtbWttmb−−=020de2v)1(e21220−=−tmbWmv0v

xotbttxbdddd2−=−=vv10第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回=rFWdtmFddtv=而21222121vvmm−=三质点的动能定理vvv

vd21=mWsFrFddtt==1vABθ2vFrd11第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回➢功是过程量，动能是状态量；注意合外力对质点所作的功，等于质点动能的增量——质点的动能定理1k2k21222121E

EmmW−=−=vv➢功和动能依赖于惯性系的选取，但对不同惯性系动能定理形式相同．动能—因物体运动而具有的能量，是速度的函数；定义：质点的动能2kmv21E=（单位：J）12第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回速度为v的子弹，打穿一块不

动的木板后速度变为零，设木板对子弹的阻力是恒定的．那么，当子弹射入木板的深度等于其厚度的一半时，子弹的速度是（A）．(B)．(C)．(D)．讨论4v41v31v21v2113第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回例2质量为m的小球系在长为l的细

绳下端，绳的上端固定，先使细绳保持水平静止，然后使小球自由下落，求细绳与水平方向成θ角时，小球的速率v和细绳所受的张力T。dcosmgldscosmgrdgmdW===sinmgldcosmglW0==因为张力不做功，由动能定理：

2kmv21EW==singl2m/W2v==lvmmasinmgT2n==−sinmg3T=求得：重力对小球所做的功：olABθθTgmrdd14第2章质点动力学2-6功和能机械

能守恒定律南通大学NantongUniversity返回1、重力的功、重力势能：一质点在重力场中沿曲线由A运动到B，则重力做功：==BABAdscosmgrdgmW重)mghmgh(dhmg0hh0−−=−=结论：重力做功与路径无关，只和质点的始、末位置有关。因此：可定义一个

与质点在重力场中位置（高度）有关的物理量，称为重力势能。mghEp=pppEEEW−=−−=)(0重➢重力对质点所做的功等于质点重力势能增量的负值。hh0ABdhθxyogmrd四质点系的功能原理15第2

章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回2、引力的功、引力势能：MmABpθdrFrdArrBr质量为m的质点在质量为M的质点的万有引力作用下沿曲线运动。m所受的引力为：2rmMGF=

−===BArr2BABAdrrGmMdscosFrdFW引−−−−=−−=)rGmM()rGmM(rGmMABrrBA引力势能的零点通常取在无穷远处。而空间某点处的引力势能定义

为：将质点从该点移至无穷远处（势能零点）时，万有引力所做的功。结论：引力做功与路径无关，只和质点的始、末位置有关。16第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回−−−−=

)rGmM()rGmM(WAB引令，则A点的引力势能为：→BrApArGmME−=ppApBE)EE(W−=−−=引➢引力对质点所做的功等于质点引力势能增量的负值。地球表面的物体所受的重力即为万有引力，在地面

上不太高的h处，引力势能为：mghhRGMm)R1hR1(GmME2EEp=−+−=其中：22Es/m80.9RGMg=即为地球表面附近的重力加速度。17第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回•已知地球质量为M

，半径为R．一质量为m的火箭从地面上升到距地面高度为2R处．在此过程中，地球引力对火箭作的功为______________．讨论5)131(RRGMm−：答案RGMm32−即：18第2章质点动力学2-6功和能机械能守恒定律南通大学

NantongUniversity返回3、弹性力的功、弹性势能：设弹簧自然伸长时，质点处在o点。由胡克定律：kxf−=当质点从x0运动到x时，弹性力做功：−−=−=xx2020)kx21kx21(xdxkW弹xOl0xfx0结论：弹性力做功与路径无关，只和质点的始、末位

置有关。定义：弹性势能2pkx21E=p0ppE)EE(W−=−−=弹➢弹性力对质点所做的功等于质点弹性势能增量的负值。19第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回•有一劲度系数为k的轻

弹簧，原长为l0，将它吊在天花板上．当它下端挂一托盘平衡时，其长度变为l1．然后在托盘中放一重物，弹簧长度变为l2，则由l1伸长至l2的过程中，弹性力所作的功为•(A)．(B)．•(C)．(D)．讨论6−21dllxkx21dllxkx−−−0201dllllxkx−−0201dllll

xkx20第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回4、保守力和势能：“任意两点间做功与路径无关”与“沿任意闭合路径做功为零”这两种说法是等效的。ABxyoL1

L2rdFrdFrdF21LABLBA+=0rdFrdF21LBALBA=−=满足上式的作用力称为保守力，即：0rdF=保保守力做功与路径无关，说明在保守力场中存在一个仅由空间位置决定的物理量，该物理量即为势能。由前面讨论知：保守力做功等于势能增

量的负值。p0ppE)EE(W−=−−=保21第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回势能具有相对性，势能大小与势能零点的选取有关．势能差与势能零点选取无关．),,(ppzyxEE=势能是状态的

函数势能是属于系统的．讨论==0),,(pp0d),,(EzyxrFzyxE00p=E令势能计算pp0p)(EEEW−=−−=22第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回pEzOzmgE=p势能曲线弹性势能曲线0,0p=

=Ex重力势能曲线0,0p==Ez引力势能曲线0,p=→ErxOpE2p21kxE=xOpErmmGE'p−=23第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回5.质点系的动能定理：1ij外iF外1F外jFi1F1iF

1jFijFjiFj1F)ij(FFFFFn1jijiiii+=+==外内外kin1jBAijBAiBAiiErdFrdFrdFWiiiiii=+===外第i个质点所受外力和内力之和：由

质点的动能定理：kn1ikin1in1jBAijn1iBAin1iiEE)rdF(rdFWWiiii==+=======外外力的功内力的功外力和内力对质点系所做的功等于质点系动能的增量。质点系的动能定理：24第2章质点动力

学2-6功和能机械能守恒定律南通大学NantongUniversity返回质点系的动量定理和动能定理的比较：内力对质点系所做的功可以改变质点系的动能。内力对质点系的冲量不改变质点系的动量。1ij外iF外1F外jFi1F1iF1jFijFjiFj1FdtF

dtFIdIdIdjiijjiij+=+=内0dt)FF(ijij=−=ijirdijFjiFjrdjijiijrdFrdFdW+=内虽然：ijijFF−=但是一般：jirdrd所以：dW内一般不等于零。25第2章质点动力学2-6功和能机械能守恒

定律南通大学NantongUniversity返回•一质点在几个外力同时作用下运动时，下述哪种说法正确？•(A)质点的动量改变时，质点的动能一定改变．•(B)质点的动能不变时，质点的动量也一定不变．•(C)外力的冲量是零，外力的功一定为零．•(D)外

力的功为零，外力的冲量一定为零．讨论726第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回根据质点系的动能定理：定义：系统的总动能和总势能之和称为系统的机械能。质点系的功能原理：外力和非保守内力对质点系所做的

功等于系统机械能的增量。k0kkEEEWWWWWW=−=++=+=保内非保内外内外p0ppE)EE(W−=−−=保内)EE()EE(WW0p0kpk+−+=+非保内外pkEEE+=EEEWW0=−=+非保内外6

.质点系的功能原理27第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回五机械能守恒定律当0inncex=+WW0EE=时，有——只有保守内力作功的情况下，质点系的机械能保持不变．pkEE−=)(0pp

0kkEEEE−−=−pkEEE+=守恒定律的意义说明28第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回•如图所示，子弹射入放在水平光滑地面上静止的木块而不穿出．以地面为参考

系，下列说法中正确的说法是（A）子弹的动能转变为木块的动能．（B）子弹─木块系统的机械能守恒．（C）子弹动能的减少等于子弹克服木块阻力所作的功．（D）子弹克服木块阻力所作的功等于这一过程中产生的热．讨论8v29第2章质点动力学2-6功和能机械能守恒定律南通大学Nantong

University返回考虑下列四个实例．你认为哪一个实例中物体和地球构成的系统的机械能不守恒?(A)物体作圆锥摆运动．(B)抛出的铁饼作斜抛运动（不计空气阻力）．(C)物体在拉力作用下沿光滑斜面匀速上升．(D)物体在光滑斜面上自由滑下．讨论930第2章质点动力学2-6功和能机械能

守恒定律南通大学NantongUniversity返回例3雪橇从高50m的山顶A点沿冰道由静止下滑,坡道AB长为500m．滑至点B后，又沿水平冰道继续滑行，滑行若干米后停止在C处.若μ=0.050．求雪橇沿水平冰道滑行的路程.31

第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回NFfFPsinPcosPh's已知,m500,050.0,m50===s'h求.s解)(cosfss'mgmgss'mgW+−−−=mghEE−=−12

m500=−=s'hs12fEEW−=32第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回例4一轻弹簧,其一端系在铅直放置的圆环的顶点P，另一端系一质量为m的小球,小球穿过圆环并在环上运动(μ=0)．开始球静止于点A,弹簧处于自然状态，其长为环半径R

;30oPBRA当球运动到环的底端点B时，球对环没有压力．求弹簧的劲度系数．33第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回解以弹簧、小球和地球为一系统BA→只有保守内力

做功系统ABEE=即)30sin2(2121o22−=+mgRkRmBvRmmgkRB2v=−又Rmgk2=所以取点B为重力势能零点0p=E30oPBRA34第2章质点动力学2-6功和能机械能守恒定律南通大

学NantongUniversity返回例5质量分别为m1和m2的两块木板用质量可忽略的弹簧相连并置于地上。求对上面的木板必须施以多大的正压力，才能使该力撤去后上面的木板跳至最高点时，下面的木板刚好能被提离地面。Fm1m2x1x2Nox取弹簧自然伸长时

m1的位置为弹性势能和重力势能的零点。上板受压时：11kxgmF=+上板跳至最高点时，N=0：22kxgm=由机械能守恒：)3(gxmkx21gxmkx2121221121+=−)2(kgmx22=)1(kgm

Fx11+=35第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回将(1)、(2)、两式代入(3)式并化简得：0g)mm2m()Fgm(gm2)Fgm(21221121=+−+−+解上式得：g)mm(F21+=讨论：由最后结果看，若交换m1、m2，结果不

变。Fm1m2x1x2Nox36第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回CpFFii=inex一般情况碰撞1完全弹性碰撞动量和机械能均守恒2非弹性碰撞动量守恒，机械能不守恒3完全非弹性碰撞动量守恒，机械能不守恒六碰撞37第2章质点

动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回完全弹性碰撞（五个小球质量全同）38第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回例6设有两个质量分别为和，速度分别为和的弹性小球作对心碰撞，两球的速度方向相同．若碰撞是完全弹

性的，求碰撞后的速度和．20v2m1m10v1v2v1v2vA1m2m10v20vBAB碰前碰后39第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回解取速度方向为正向,由机械能守恒定律得2222112202210121212121vvvvmm

mm+=+)()(220222212101vvvv−=−mm2211202101vvvvmmmm+=+由动量守恒定律得1v2vA1m2m10v20vBAB碰前碰后(2))()(20221101vvvv−=−mm(1)40第2章质点动力学2-6功

和能机械能守恒定律南通大学NantongUniversity返回21202102112)(mmmmm++−=vvv21101201222)(mmmmm++−=vvv由、可解得：202110vvvv+=+12

2010vvvv−=−(3)(2)(1)由、可解得：(3)(1)1v2vA1m2m10v20vBAB碰前碰后41第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回（1）若21mm=则102201,vvvv==则0,2101−vv

v讨论12mm（3）若,且020=v1021012,vvvv则（2）若020=v12mm,且1v2vA1m2m10v20vBAB碰前碰后42第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回两个质子

发生二维的完全弹性碰撞43第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回•例7用一个轻弹簧把一个金属盘悬挂起来(图2—18)，这时弹簧伸长了。一个质量和盘相同的泥球，从高于盘处由静止下落到盘上。求此盘向下运动

的最大距离。cml101=cmh30=2l2l解：本题可分为三个过程进行分析44第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回泥球自由下落过程：机械能守恒ghv2=泥球和盘的碰撞过程：动量守恒Vmmmv)(+=泥球和盘共同下降的过程：机械能守

恒2212122)(2121)2()2(21llkklglmVm+=++cml302=可得：45第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回德国物理学家和生理学家．于1874年发表了《论力(现称能量)守恒》的演讲，首先系统地以数学方式阐述了

自然界各种运动形式之间都遵守能量守恒这条规律．是能量守恒定律的创立者之一．亥姆霍兹(1821—1894)46第2章质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回能量守恒定律：对一个与自然界无任何联系的系统来说,系统内

各种形式的能量可以相互转换，但是不论如何转换，能量既不能产生，也不能消灭。（1）生产实践和科学实验的经验总结；（2）能量是系统状态的函数；（3）系统能量不变,但各种能量形式可以互相转化；（4）能量的变化常用功来量度．47第2章

质点动力学2-6功和能机械能守恒定律南通大学NantongUniversity返回下列各物理量中，与参照系有关的物理量是哪些？（不考虑相对论效应．）(1)质量(2)动量(3)冲量(4)动能(5)势能(6)功答动量、动能、功．讨论1048